Funktionenscharen Nullstelle Funktion angeben

Question

Aufgabe: Funktionscharen

Text erkannt:

geschützt.

Gerade bei der mathematischen Modellierung realer Probleme entsteht nicht nur die Abhängigkeit von einer Variablen \( \mathrm{x} \), sondern von weiteren Variablen, die man als Parameter in die Funktion einbringt.

Oft ist es auch sinnvoll, bewusst Parameter einzubringen, um deren Einfluss auf die Funktion zu untersuchen.
Einstiegsaufgaben zu Funktionenscharen
Aufgabe 1:
Gegeben ist eine Funktionenschar \( f_{k}(x) \) mit \( f_{k}(x)=\frac{2}{k} x+k \).
a) Gib die Funktionen für \( k=1 ; k=2 ; k=3 \) und \( k=4 \) an.
b) Zeichne die zugehörigen Graphen und beschrifte sie.
c) Bestimme die Nullstellen der Funktionen aus a).
Stell dir vor, du hättest für noch viel mehr Funktionen aus der Funktionenschar die Nullstellen bestimmen müssen - da wäre es doch ganz schön lästig, jede Funktionsgleichung einzeln umzuformen. Versuche doch einmal folgendes:
d) Gib eine allgemeine Formel an, die dir zu jedem belieben Wert für \( k \) die Nullstelle angibt. Überprüfe deine Formel anhand der Ergebnisse aus c).
Aufgabe 2:
Gegeben ist eine Funktionenschar \( f_{k}(x) \) mit
i) \( f_{k}(x)=k x^{2}-4 \)
ii) \( f_{k}(x)=(x-k)^{2}-k \)
Bearbeite zu diesen Scharen jeweils die Aufgabenteile a), c) und d) aus der 1. Aufgabe. Hier wäre allerdings sicherlich eine andere Reihenfolge sinnvoll.

wie löst man das schritt für schritt danke schonmal

Answer 1

1. 2/k*x +k= 0

2/k*x = -k

x = -k^2/2

2. kx^2-4 = 0

kx^2= 4

x^2 = 4/k

x= +- 2/√k

(x-k)^2 -k =0

(x-k)^2 = k

x-k = +-√k

x = +-√k +k

Answer 2

Hallo,

\(f_k(x)=\frac{2}{k}x+k\)

a) Gib die Funktionen für \( k=1 ; k=2 ; k=3 \) und \( k=4 \) an.

Setze die entsprechenden Werte ein:

\(f_1(x)=\frac{2}{1}x+1=2x+1\\ f_2(x)=\frac{2}{2}x+2=x+2\)

Für k = 3 bzw. 4 verfährst du ebenso.

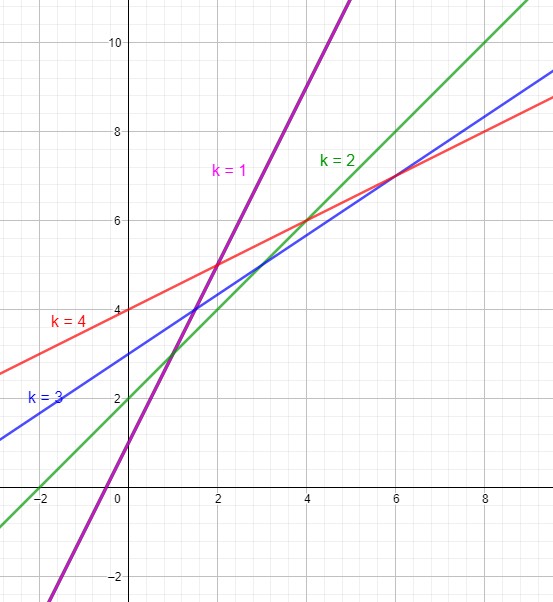
b) Zeichne die zugehörigen Graphen und beschrifte sie.

Das könnte so aussehen:

c) Bestimme die Nullstellen der Funktionen aus a).

Setze die Funktionen = 0 und löse nach x auf. Für k = 1 sieht das so aus:

\(2x+1 = 0\\ 2x=-1\\ x=-\frac{1}{2}\)

d) Gib eine allgemeine Formel an, die dir zu jedem belieben Wert für \( k \) die Nullstelle angibt. Überprüfe deine Formel anhand der Ergebnisse aus c).

Behandle k wie eine beliebige Zahl.

\(\frac{2}{k}x +k=0\quad |-k\\ \frac{2}{k}x=-k\quad |:\frac{2}{k}\\ x=-\frac{k^2}{2}\)

Gruß, Silvia