So wie man immer den Schnittpunkt zweier Funktionen berechnet. Man setzt sie zunächst gleich und löst nach \(x\) auf. Zugegebenermaßen ist das vielleicht das Problem ...
$$\sin x = \cos x \quad \Rightarrow x=?$$ Kenner der trigonometrischen Funktionen wissen, dass die Lösungen bei \(x_1=\pi/4\) und \(x_2=5\pi/4\) liegen. Das folgt schon aus der Anschauung im Einheitskreis.
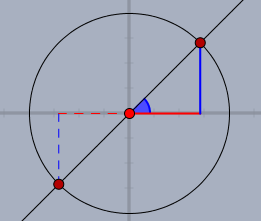
Der Cosinus (rot) und der Sinus (blau) sind genau auf der Winkelhalbierenden der X- und Y-Achse gleich - d.h. bei \(45°=\pi/4\). Aber wie kommt man darauf, wenn man es nicht 'sieht'?
Dann sollte man wissen, dass \(\cos^2 x + \sin^2 x=1\) ist. D.h. man kann den Cosinus in den Sinus umrechnen. Und wenn Sinus und Cosinus gleich sind, so muss das auch für die Quadrate gelten - also ist
$$\cos^2 x = \sin^2 x = 1 - \cos^2 x \quad \Rightarrow \cos^2x = \frac{1}{2}$$
$$\space \Rightarrow \cos x = \pm \frac12 \sqrt{2} \quad \Rightarrow x_{1,2} = \pm \frac{\pi}{4}; \quad x_{3,4}=\pm \frac{3}{4}\pi$$Sinus und Kosinus müssen aber immer das selbe Vorzeichen haben, sonst wären sie nicht gleich, deshalb fallen noch zwei der Lösungen raus und man erhält die oben schon genannten Lösungen.