Hallo Dramaqueen,
zur Beantwortung beider Fragen betrachtet man die Gewinnfunktion:
G(x) = E(x) - K(x) = 60·x - (0.03·x3 - 2·x2 + 50·x + 600) = - 0.03·x3 + 2·x2 + 10·x - 600
a)
Der BEP (= Gewinnschwelle) ist die kleinste Produktionsmenge x1, ab der (x > x1) ein Gewinn erwirtschaftet wird. Das ist hier die erste positive Nullstelle von G(x).
G(x) = 0 ergibt (Rechner): x1 ≈ 16.988
[ ∨ x = -17.5196 ∨ x = 67.19 ] (#)
Da die Produktionsmenge in "Stück" angegeben ist: x1 ≈ 17
b)
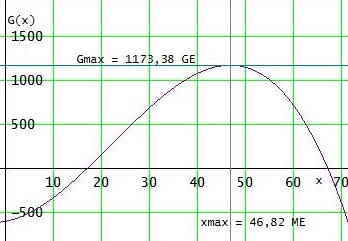
Den maximalen Gewinn hat man beim Hochpunkt H(xmax | Gmax) von G(x) bei der Produnktionsmenge xmax.
xmax ist hier die positive Nullstelle der Ableitung von G'
G'(x) = - 0.09·x2 + 4·x + 10 = 0 →pq-F xmax ≈ 46,818
Wegen G(46) ≈ 1171.92 > 1173.31 ≈ G(47) xmax ≈ 46 [Stück !]
-------
(#)
Mit einem normalen TR kann man diese Nullstellen z.B. mit dem Newtonverfahren (Näherungsverfahren) ausrechnen.
Gruß Wolfgang