Mathematik Nullstellen der Sinusfunktion

Question

Periode = pi/ 2 und mein Wertebereich [-1/7]

Wie berechne ich nun die nullstellen einer sin Funktion? Wie kann ich dadurch meine gleich stellen und dann Substitution usw weiter zu rechnen?

Comments

Wieso werden hier Nullstellen benötigt? Hast du nur einen Teil der Aufgabe fotografiert? :-/

Answer 1

Hallo Maria,

f(x) = sin(b·x)   mit Periode 2π/ b = π/2  →  b = 4

f(x) = sin(4·x)

> Wie berechne ich nun die Nullstellen einer sin Funktion?

 sin(4·x) = 0         

    die Nullstellen von sin(x) sind alle ganzzahligen Vielfachen von π:

 4x = k · π   →  x_k = k · π/4      mit k ∈ ℤ

für den Wertebereich  [ -1 ; 7]  musst du jetzt die passenden  k-Werte suchen:

mit k = -1, 0, 1, ..... , 8   erhältst du jeweils eine Nullstelle von f

-----

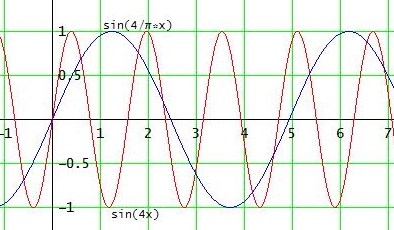
Bei Streckung mit dem Faktor π in x-Richtung   hat man f₂(x) = sin( 4/π·x ) mit der Periode π²/2

Gruß Wolfgang

Answer 2

Hallooo MariiiiiaaaaLaaaa ! :-D :-)

Eine Notwendigkeit, die Nullstellen zu berechnen, erkenne ich bei dieser Aufgabe nicht. :-O

T: Periode
Gegeben: T = π/2
b = 2π/T
b = 2π/(π/2) = 4

Gegebener Wertebereich von y=-1 bis y=7 (kann man auch -1 <= y <= 7 schreiben).
Die Sinusfunktion pendelt um ihre Ruhelage y = (-1 + 7)/2 = 3, wir müssen die Sinusfunktion
um 3 Einheiten nach oben verschieben. Der Parameter d=3 tut erledigt das für uns.
Der Maximalwert ist y=7, die Ruhelage liegt bei y=3, damit ist die Aplitude a= 7-3 = 4.
Unsere mögliche Funktionsgleichung ist fertig: f(x) = a sin(bx) + d wird mit den berechneten Paramtern zu
f(x) = 4 sin(4x) + 3

Der Graph soll entlang der x-Achse gestreckt werden. Das ist mit einem Faktor -1 < b < 1 möglich.
Mit dem Faktor π lässt sich der Graph nicht strecken, lediglich stauchen. Diese Aufgabe ist irreführend :-(
Eine Streckung wäre mit 1/π  =  0,318.. möglich. Der Faktor ist dann aber 1/π und nicht π.
Dann würde die Funktionsgleichung f(x) = 4 sin(4/π x) + 3 der gewünschten Eigenschaft entsprechen.

Beste Grüße