Bei der Produktion von Fahrrädern fallen in jeder Woche 8.000€ Fixkosten an. Die variablen Kosten betragen pro Rad 800€. Das Unternehmen erzielt auf dem Markt einen Preis je Rad von 1.350€. Zurzeit kann der Betrieb höchstens 25 Räder pro Woche herstellen.
a) Erstellen Sie die Kosten- und Erlösfunktion
K(x) = 8000 + 800x
E(x) = 1350x
b) Berechnen Sie die Gewinnschwelle (Break-even-point)
E(x) = K(x)
1350x = 8000 + 800x
x = 160/11 = 14.5
c) Geben Sie die Gewinnfunktion G an
G(x) = E(x) - K(x) = 550·x - 8000
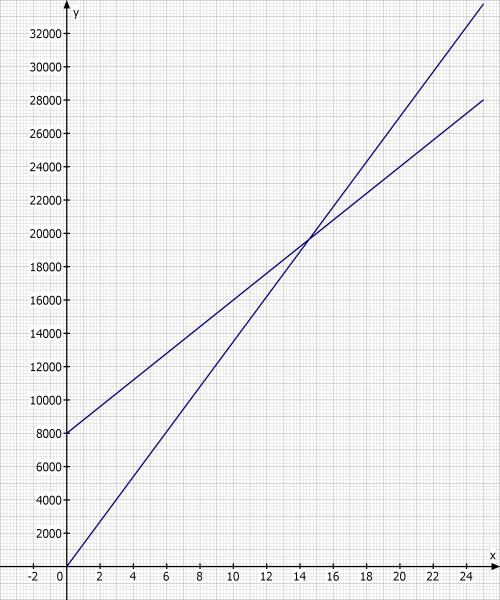
d) Stellen Sie die Kosten- und Erlösfunktion in einem Schaubild dar.