sinus und cosinus Periode

Question

Berechne die Nullstellen/Perioden:

f(x) = sin( πx ) + cos( 2πx ) + 1

Habe 3 Werte:

x1 = π

x2 = π + 1

x3 = 1/π + 1

Bin mir aber nicht sicher ob die Werte stimmen.

Vielen Dank

Comments

Eine Nullstelle ist ungefähr 1,284514. Also keine von deinen.

---

Also keine von deinen

Aber deine auch nicht.
Und rede dich nicht damit heraus, du hättest ja "ungefähr" geschrieben.

---

Ok, ok: ungefähr 1.285176. Zufrieden?

---

Warum denn nicht gleich so !

---

Eine Rechnung würde mir sehr weiterhelfen.

---

Ich vermute mal, man muss cos(2πx) mit einem Additionstheorem umformen und dann noch einige weitere Umformungen vornehmen. Ziel sollte sein, eine einzige Winkelfunktion mit nur einem Winkelargument zu erhalten.

Answer 1

Hallo Jackson,

f(x) = sin( πx ) + cos( 2πx ) + 1

Periode  2π/π = 2  ,  Periode 2π/2π  = 1  

→  Periode von f   ist das kvV  von 1 und 2  = 2 

Für die Nullstellen  von f übernehme ich von Mathef

 sin( πx ) + cos( 2πx ) + 1 = 0  

⇔   sin(π*x) = 1/4  ± √(17/16) ,   wobei    1/4  + √(17/16) > 1  entfällt

 sin(π*x) = 1/4 - √(17/16)     | arcsin ( TR = sin^-1 )

π * x  ≈ - 0.8959074812  + k * 2π    oder   π * x =  π - (- 0.8959074812)  + k * 2π    | : π

x  ≈   - 0.2852 + 2k   oder  x  ≈  1.2852 + 2k     ( mit  k ∈ℤ ) 

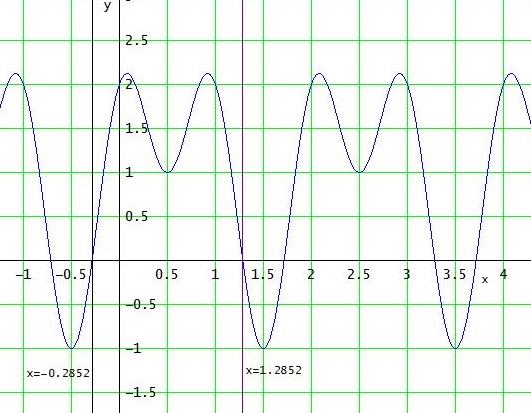
Gruß Wolfgang

Answer 2

sin(pi*x) + cos( 2*pi*x) +1 = 0     (Formel für cos(2*y) nehmen)

<=>  sin(pi*x) + 1 - 2sin²(pi*x) +1 = 0

<=>   - 2sin²(pi*x) + sin(pi*x) + 2 = 0 | :-2

<=>   sin²(pi*x) -0,5* sin(pi*x)  - 1  = 0    Substitution  sin(pi*x)=z gibt

z² -0,5z -1 = 0   also z = 1/4   ± √(17/16)

Und jetzt mit   sin(pi*x)= 1/4   ± √(17/16)     weiter

gibt mehrere Lösungen z.B. etwa 1,71 oder 1,29  oder -0,285  etc.