Hallo Leonie,
Das Verhältnis von Seite und Diagonale eines Fünfecks ist der sogenannte Goldene Schnitt. Wenn man also die Diagonale mit der Konstruktion des goldenen Schnittes teilt, erhält man die Seitenlänge und der Rest geht über einfache Dreieckskonstruktionen. Die Konstruktion des goldenen Schnitts findest Du z.B. hier.
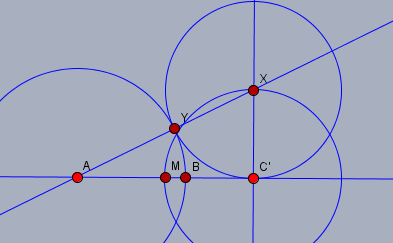
Die Strecke \(AC'\) ist gegeben. Zeichne eine Senkrechte in \(C'\) und trage die Hälfte von \(AC'\) dort ab. man bekommt den Punkt \(X\). Jetzt um \(X\) einen Kreis mit Radius \(XC'\), der die Strecke \(AX\) in \(Y\) schneidet. Der Kreis \(k_3\) um \(A\) mit Radius \(AY\) schneidet \(AC'\) in \(B\). \(B\) sei bereits ein Punkt des Fünfecks.
Jetzt weiter mit einem Kreis um \(B\) mit Radius \(AB\), der den Kreis \(k_5\) um \(A\) mit Radius \(AC'\) in \(C\) schneidet (beide hellblau).
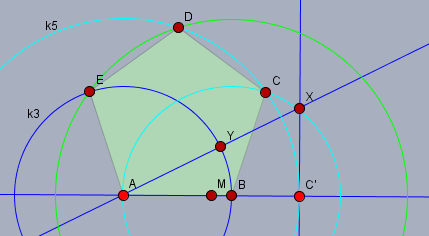
Der Kreis um \(B\) mit Radius \(AC'\) (grün) schneidet \(k_5\) in \(D\) und \(k_3\) (blau) in \(E\). \(ABCDE\) ist das fertige Fünfeck.
Gruß Werner