\(t=1\) und nicht 2! Und
$$\begin{pmatrix}5 \\-1 \\ 4\end{pmatrix} \ne A$$
Es muss heißen:
$$g(t=1)= \space \begin{pmatrix}1 \\1 \\ 0\end{pmatrix} + 1 \cdot \begin{pmatrix}2 \\-1 \\ 2\end{pmatrix} = \begin{pmatrix}3 \\0 \\ 2\end{pmatrix}=A$$
Du fragtest: "doch warum gilt hier diese Formel(unten) nicht: statt a und b Richtungsvektor u und normale n nehmen"
Die Formel gilt immer! Wenn das Skalarprodukt zweier Vektoren =0 ist, so stehen sie senkrecht auf einander. Nur - das war nicht die Frage!
Die Frage war:"Steht die Gerade \(g\) senkrecht auf \(E\)?" es ist ganz wichtig, dass Du Dir klar machst, was die einzelnen Vektoren und Größen in diesen Formeln bedeuten. Wenn Du das nicht verstehst, dann hast Du zum einen Schwierigkeiten, die Aufgaben zu machen und (viel schlimmer) Du wirst alles vergessen, nachdem der Stoff in der Schule abgearbeitet wurde. D.h. Dein ganzes Lernen war umsonst!
Zu den Vektoren ein kleine Skizze:
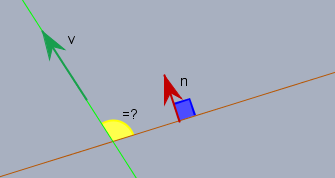
Du siehst dort die grüne Gerade \(g\) mit dem Richtungsvektor \(v\). Sowie einen Schnitt durch die Ebene \(E\) (braun) und ihren Normalenvektor \(n\) , der bereits senkrecht auf \(E\) steht.
Wie müssen jetzt \(v\) und \(n\) zu einander stehen, damit der Winkel zwischen \(g\) und \(E\) (der gelbe) ein rechter ist?
Du schriebst: ".. stimmt es jetzt ? oder fehlt da noch etwas?" Nein, es stimmt nicht und Ja, es fehlt noch was. Die Gleichung für \(\delta\) lautet:
$$\begin{aligned} \delta &= \frac{n \cdot a -b}{n^2} \\ &=\frac{(4\cdot 3 + (-2)\cdot 0+ 2\cdot 4)- 11}{4^2 + (-2)^2+ 4^2} \\ &=\frac{9}{36}=\frac{1}{4} \end{aligned}$$
Ohne Betragsstriche und mit \(n^2\) im Nenner. Und das was bei Dir fehlt ist der gesuchte Punkt \(a'\) auf der Ebene:
$$a'=a - \delta \cdot n = \begin{pmatrix}3 \\0 \\ 2\end{pmatrix} - \frac{1}{\colorbox{#F0F000}{4}} \begin{pmatrix}4 \\-2 \\ 4\end{pmatrix}= \begin{pmatrix}2 \\0,5 \\ 1\end{pmatrix}$$
Setze die Koordinaten in die Ebenengleichung ein, und Du wirst sehen, dass es aufgeht.
Edit: Tippfehler korrigiert \(\frac12 \text{ nach } \frac{1}{\colorbox{#F0F000}{4}}\)