Aufgabe:
Berechnen Sie den Punkt S der Stange sowie ihren Abstand zur x1x2-Ebene.
Problem/Ansatz:
Zur Homeoffice Bearbeitung im Matheunterricht wurde folgende Aufgabe gestellt:
Die Terrasse liegt in der x1x2-Ebene. In den Punkten A (-10/-22/26) und (-14/-10/24) der Hauswand soll ein Sonnensegel befestigt werden, dessen äußere Eckpunkte bei Straffung des Segels B (20/32/23) und C(19/35/22,5) sind (1 Längeneinheit entspricht 1 dm).
a) Zeigen Sie, dass das Segel die Form eines Trapezes hat. Prüfen Sie, ob das Trapez gleichschenklig ist.
b) Das Segel wird an einer Stange mit Spitze S befestigt. Berechnen Sie, wie hoch die Stange sein muss und in welchem Punkt der x1x2-Ebene sie aufgestellt werden muss.
Ich kämpfe momentan mit b). Und zwar hab ich die Geradengleichungen für die Vektoren zwischen AB und DC aufgestellt und möchte den Schnittpunkt berechnen. Bei der Berechnung treffe ich aber auf negative Werte für die Parameter für den Schnittpunkt, und das macht ja keinen Sinn. Anbei ein Bild zur Veranschaulichung und meinen Arbeitsfortschritt bis jetzt.
Wenn jemand mich auf einen möglichen Fehler aufmerksam machen könnte wäre ich sehr dankbar!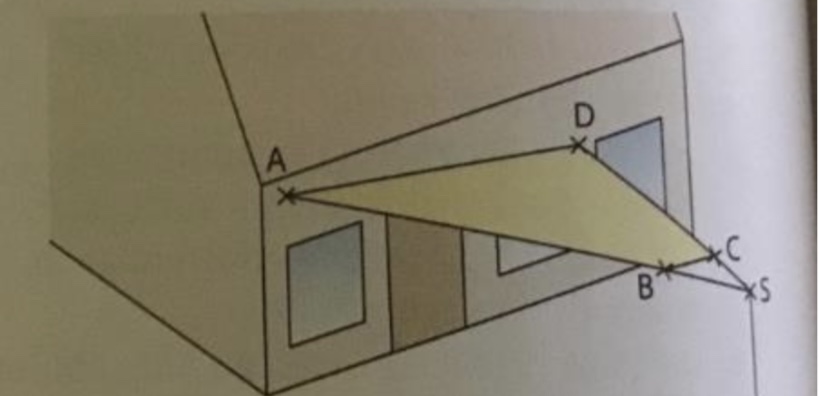
Text erkannt:
\begin{tabular}{l}
(年) \\
\hline
\end{tabular}
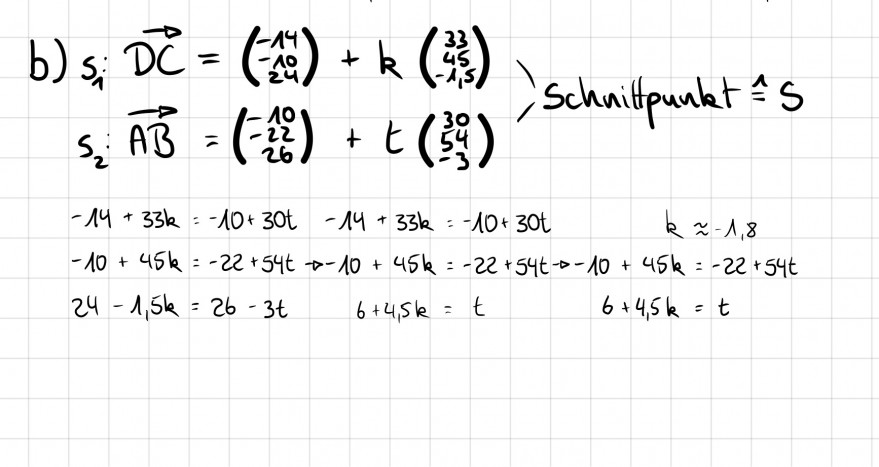
Text erkannt:
\( s_{i} \overrightarrow{A B}=\left(\begin{array}{c}-10 \\ -22 \\ 26\end{array}\right)+t\left(\begin{array}{c}30 \\ -3\end{array}\right) \)
\( -14+33 k=-10+30 t-14+33 k=-10+30 t \)
\( -10+45 k=-22+54 t-10+45 k=-22+54 t-8-10+45 k=-22+54 t \)
\( 6+45 \mathrm{k}=\mathrm{t} \)
\( 6+45 \mathrm{k}=\mathrm{t} \)