Vereinfachung des Termes x(x+h)

Question

Kann mir jemand zeigen wie dieser Term auf diese Form vereinfacht werden konnte?

Das obere x-(x+h) verstehe ich, aber dieses untere x*(x+h) verstehe ich nicht. 

Answer 1

:-)

Die ursprüngliche Aufgabe war wohl den Term 1/(x+h) - 1/x auf den Hauptnenner zu bringen.

Dabei wurde der "Trick" benutzt, dass sich ein Bruch(generell ein Zahlenwert) nicht ändert wenn man ihn mit 1 multipliziert:
1/(x+h) * 1 = 1/(x+h) * x/x und
1/x * 1 = 1/x * (x+h)/(x+h)
Nach Anwendung der Rechenregeln für Brüche folgt die Darstellung (x-(x+h)) / (x*(x+h))

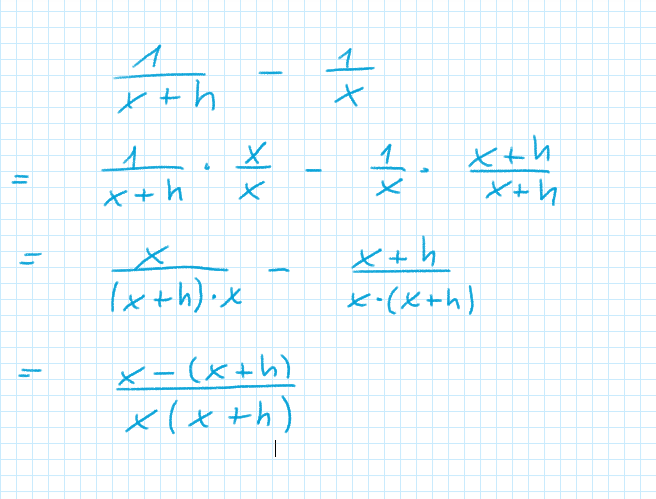
Beste Grüße

P.S.

dieses untere x*(x+h) verstehe ich nicht.
Das ist der Hauptnenner

Answer 2

x/x=1 und (x+h)/(x+h)=1. Also steht da 1/(x+h)-1/x. Auf den Hauptnenner x(x+h) bringen und subtrahieren. Dann ist der Zähler x - (x+h).

Answer 3

Der Nenner für beide Brüche ist bereits gleich
x * ( x + h )

allgemein
a / b - c / b = ( a - c ) / b

Comments

x * (x+h)  =  (x+h) * x 

Warum allgemein, wenn es oben schon explizit steht ? 

Answer 4

https://de.serlo.org/20317/addition-subtraktion-gleichnamige-brueche