Hinführend zu Integralrechnung

Question

 Ich habe einmal eine Frage wir sollen ja einfach den Flächeninhalt ausrechnen ... 

Ich bin mir nicht ganz sicher wie ich das machen soll, wahrscheinlich ist das zu simpel :/ brauch man die Funktionsgleichung da überhaupt für ? 

Wäre wirklich lieb wenn mir das einer erklären könnte, weil ich irgendwie gerade voll das Brett vorm Kopf habe !-.-

Comments

Wenn ihr gerade bei der Einführung zur Integralrechnung  seit, dann sind die Flächen bestimmt erstmal geometrisch zu berechnen. Verwende hierzu Rechtecke und Dreiecke. Später kannst du diese Ergebnisse dann auch mithilfe der Integralrechnung bestätigen.

---

"Ist es denn dann für alle Funktionen gleich bei (0;b) und (a;b) das verstehe ich noch nicht so ganz ... also das mit dem zahlen habe ich verstanden, aber ich habe Probleme damit, wenn die nicht gegeben sind:/"

Wenn die Graphen nicht aus Geradenstücken bestehen (z.B. bei f(x) ?= x^2) kann man dann nicht mehr einfach so Dreiecks-, Trapez- und Rechtecksflächen benutzen. Erst dann brauchst du die Integration. 

Answer 1

usw. 

Die Aufgabe besteht aus 4*5 = 20 Teilaufgaben. Wenn du geschickt vorgehst, brauchst du nur Häuschen zu zählen. 

Hier nochmals dasselbe vereinfacht gerechnet:

Comments

> ... 4*5 = 20 Teilaufgaben. Wenn du geschickt vorgehst, brauchst du nur Häuschen zu zählen. 

Über dem Intervall [a,b] dürfte das etwas schwierig werden :-)

z.B. bei 3)

A = b²/2 - a²/2   (vgl. meinen Kommentar unter meiner Antwort)

Answer 2

Hallo nobody,

in der Aufgabenstellung ist erst einmal von einem Integral keine Rede.

Alle Flächen stellen entweder ein Rechteck ein Dreieck oder ein Trapez dar. Letztere lassen sich in ein Rechteck und ein Dreieck zerlegen. Du kannst also alle Flächen einfach geometrisch ausrechnen.

An den Ergebnissen mit a und b lassen sich dann später Zusammenhänge mit einer Stammfunktion der jeweiligen Funktion erkennen.

Z.B. beträgt die Fläche, die du bei 3) markiert hast:  

A_Quadrat + A_Dreieck  =  (4-2) * 2 + 1/2 * (4-2) * 2

Oder über [a,b]:    (b-a) * f(a) + 1/2 * (b-a) * ( f(b) - f(a) )      , Dreieckhöhe

Gruß Wolfgang

Comments

Vielen Dank ! Ja genau, wir sollen die erstmal ganz normal berechnen.

Die funktionsgleichung spielt dann keine Rolle oder? 

---

Für die Berechnung Über das Flächenintegral benötigst du die Fkt, um dann F(x) also die Stammfunktion zu bilden.

---

@nobody

Du benötigst die Funktionsgleichung hier (ohne Integralrechnung!), wenn du die benötigten Längen bei [a,b] mit Hilfe von f(a) und f(b) ausrechnen musst.

z.B. bei 3)  mit f(x) = x    (vgl. meine Antwort):

A = (b-a) * f(a) + 1/2 * (b-a) * ( f(b) - f(a) )   

    =  (b-a) * f(a) + 1/2 * (b-a) * ( f(b) - f(a) )  

    =  (b-a) * a + 1/2 * (b-a) * ( b - a)  

    = b²/2 - a²/2 

und das steht  später im Zusammenghang mit dem Stammfunktionsterm 

 F(x) = 1/2 x²  zu  f(x) = x 

---

Ist es denn dann für alle Funktionen gleich bei (0;b) und (a;b) das verstehe ich noch nicht so ganz ... also das mit dem zahlen habe ich verstanden, aber ich habe Probleme damit, wenn die nicht gegeben sind:/

---

A = (b-a) * f(a) + 1/2 * (b-a) * ( f(b) - f(a) )    gilt immer dann, wenn die Funktionen Geraden sind.

Wenn du das für [a,b] hast, musst du doch bei [0,b] nur a=0 einsetzen.

A = b * f(0) + 1/2 * b * ( f(b) - f(0) )   

---

 Also wäre das so dann richtig ? ( das mit Bleistift geschriebene)

Und ist das dann auch die Lösung für die anderen Grapfhen , also das ist jetzt für den 3. 

vielen Dank für deine Hilfe !!

---

3. f(x) = x kannst du einsetzen, im Lauf der Rechnung. 

[0,b]

F[0,b] = (f(0) + f(b))/2 * (b-0) = (0 + b)/2 * b = b^2/2 .

[a,b]

F[a,b] = (f(a) + f(b))/2 * (b-a) 

= (a + b)/2 * (b-a)  

= ((b+a)(b-a))/2    | 3. binomische Formel

= (b^2 - a^2)/2 

= b^2/2 - a^2/2 

Ohne Einschränkung der Allgemeinheit, kannst du annehmen, dass a<b (andernfalls umbenennen). 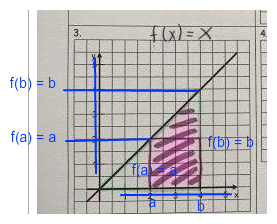Beschrifte die Achsen passend. 

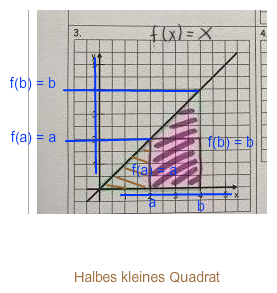
Nun kannst du die rote Fläche ausrechnen als 

(Halbes grosses Quadrat) - (halbes kleines Quadrat) 

= b^2/2 - a^2/2 

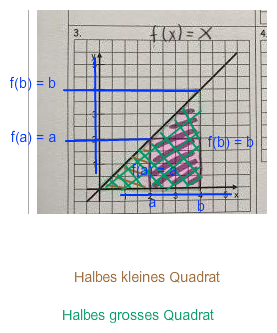
Oder mit der Umformung oben als Fläche des Trapezes mit Mittellinie m = (f(a) + f(b))/2 und Höhe (b-a) . 

Answer 3

Alle fünf Funktionen sind lineare Funktion.
a : Anfangspunkt der Fläche
b : Endpunkt der Fläche

Für alle gilt die Möglichkeit die Fläche
über die Formel des Trapezes auszurechnen
[ ( Funktionswert bei a ) + ( Funktionswert bei b )  ] / 2
mal ( b - a )

( f ( a ) + f ( b ) ) / 2   * ( b - a )

Answer 4

,[

[a,b] ist das Intervall , g(x)  sei die Stammfkt von f(x).

Comments

Wie muss ich das dann aufschreiben ?

Zb jezt bei der 1. Funktion  

A=...?

---

A = integral im [a,b] , stammfkt bilden und grenzen einsetzen s.o. , Ergebnis in [FE]

---

Das hatten wir so noch nicht wir sollen das irgendwie so aufschreiben

[0;4]  A=2*4

[2;4] A= 2*(4-2)