Volumen ist zu berechnen aus Zulauf bzw Ablauf ohne Funktionsgleichung, Integralrechnung

Question

Aufgabe:

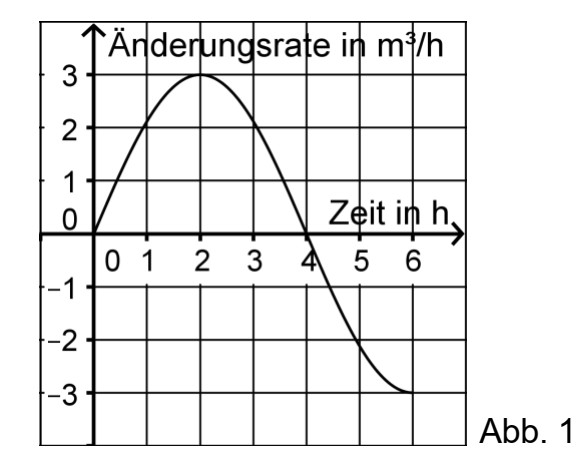
Abbildung 1 stellt für einen Wassertank die Zufluss- bzw. Abflussrate (in mh3 ) von Wasser für
einen Beobachtungszeitraum von sechs Stunden dar. Zu Beginn der Beobachtung enthält der Tank 2m3 Wasser.

Text erkannt:

Text erkannt:

a Bestimmen Sie das Volumen des Wassers, das sich zwei Stunden nach Beobachtungsbeginn im Tank befindet.

b Skizzieren Sie den Graphen, der die Entwicklung des Volumens des Wassers im Tank in Abhängigkeit von der Zeit darstellt.

Das ist eine Beispielaufgabe für eine Abituraufgabe. Als Lösung wird bei a 5,8 m3 angegeben.

Problem/Ansatz:

Beim Zulauf bzw Ablauf wird keine Funktionsgleichung angegeben. Wie soll die Aufgabe gelöst werden? Soll hier das Integral numerisch gelöst werden? Wenn ich zB die Simpson-Regel anwende, komme ich auf 5,67 m3 und nicht auf 5,8m3. Auch der Teil b gestaltet sich schwierig ohne die Bildung einer Stammfunktion? Hat jemand eine Idee, wie man die Aufgabe eleganter lösen kann?

Comments

Das ist eine Beispielaufgabe für eine Abituraufgabe.

Welches Beispiel zu welchem Abitur?

---

Wenn ich zB die Simpson-Regel anwende, komme ich auf 5,67 m3

Wie hast Du diese Regel angewendet?

Answer 1

\(\displaystyle 2+\int \limits_{0}^{2} 3 \cdot \sin \left(\frac{t}{4} \pi\right) d t \approx 5,8 \)

Comments

In der Aufgabenstellung fehlt m.E. der entscheidende Hinweis, dass es sich um eine trigonometrische Funktion handelt.

---

Das sehe ich auch so. Hast du mal einen Ansatz über eine Funktion 3. Grades probiert?

---

Vielleicht kannst du selber begründen, warum ein Ansatz über eine Funktion 3. Grades nicht gut ist.

~plot~ x^3/8-3x^2/2+4x;[[-1|9|-4|4]] ~plot~

Answer 2

Verwende die ablesbaren Punkte. Zwei davon sind Extremwerte.

Comments

Meinst du damit, dass ich eine ganzrationale Funktion 3. Grades annehmen soll, um dann die Koeffezienten zu bestimmen?

Answer 3

f(x) = 3·SIN(pi/4·x)

F(x) = - 12/pi·COS(pi/4·x)

V = 2 + F(2) - F(0)
V = 2 + (- 12/pi·COS(pi/4·2) - (- 12/pi)
V = 2 + (0) - (- 12/pi)
V = 2 + 12/pi ≈ 5.8 m³

Im hilfsmittelfreien Teil langt das Abschäzen des Flächeninhaltes des Graphen im Intervall [0 ; 2] mit ca 4. Damit würde man dann auf 6 m³ kommen.