Du schreibst: "wenn man die Punkte auf einer Geraden bestimmen muss, geht man da von einem Ortsvektor aus?" Richtig - in diesem Fall vom Vektor \(P=(1;-3;2)^T\).
Du schreibst weiter: "In der Lösung gehen die Punkte alle vom Ursprung aus.. " Nein - das tuen sie nicht. Das sieht vielleicht für Dich so aus. Die Gerade die in der Lösung durch den Ursprung verfläuft ist die X1-Achse. Zur besseren Ansicht hab ich die Punkte mal im Geoknecht3D eingezeichnet:
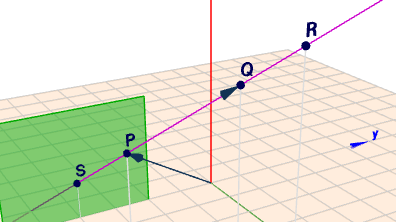
Klick hier, dann kommst Du in die Ansicht des Geoknecht3D und Du kannst die Szene mit der Maus drehen, so dass Du eine dreidimensionale Vorstellung von der Szene bekommst. Du solltest das am PC und nicht am Smartphone versuchen ;-)
Der Schnittpunkt \(S=(\colorbox{#F0F000}{0};-4;1)^T\) mit der \(x_2x_3\)-Ebene (grün) ist deshalb ein Schnittpunkt mit dieser Ebene, weil seine \(x_1\)-Koordinate =0 ist.
"Wir haben das so gelernt, dass die Punkte vom Punkt p ausgehen sollen, indem einfach ein anderes Lambda eingesetzt wird." Das ist richtig!