Definitionsbereich bestimmen und warum diese Funktion surjektiv und nicht injektiv ist.

Question

+0

Hallo ich habe eine Aufgabe gestellt bekommen die ich bis Montag lösen soll:

D_{f = [-3;3]}

f(x) : = 2/x²+1

a)Die erste Aufgabe lautet: Bestimmen sie für den vorgegebenen Definitionsbereich die Menge   W_f   ⊂ ℝ bestimmen damit 

f : D_f → W_f  , x ↦ f(x)  eine surjektive Abbildung wird.

b)und dann soll  Ich  die Frage beantworten ; warum f nicht Injektiv ist

Dabei soll ich die größt möglichen Intervalle I ⊂ D_f  angeben, auf denen die Einschränkung f _I   injektiv ist. 

Ich soll außerdem den Funktionsgraphen von f sowie die zugehörigen lokalen Umkehrfunktionen skizzieren.

Ich habe jetzt schon all meine Bücher durchgeschaut aber finde nichts, was es mir Ansatzweise erklärt. 

Also die Fachbegriffe verstehe ich und auch wann eine Funktion surjektiv und wann injektiv ist aber nicht, wie ich diese Aufgabe lösen soll :( 

:)

Answer 1

Hallo Anni,

f(x) = 2/x² + 1   D_f  = [-3;3]  \ {0}  (!)           (vgl. unten #)

f '(x) = - 4 / x³  

f '(x) < 0 für x > 0  →  f  streng monoton fallend in ] 0 ; 3 ]

f '(x) > 0 für x < 0  →  f  streng monoton steigend in [ -3 ; 0 [

lim_{x→ 0+} f(x)  =  lim_{x→ 0-} f(x)  = ∞ ;  f( ± 3) = 11/9

→  W_f  =  [ 11/9 ; ∞ [   

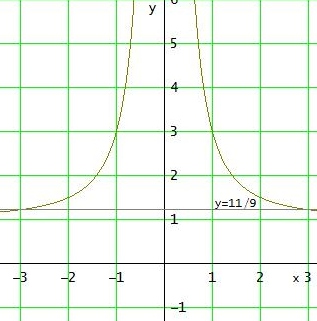
Die Funktion hat auf den größtmöglichen Teilmengen ] 0 ; 3 ] und [ -3 ; 0 [ des Definitionsbereichs für alle x-Werte verschieden Funktionwerte, ist dort also jeweils injektiv. 

Wegen f(1) = f(-1) = 2  ist sie über D nicht injektiv.

Eine Funtion  f: D → W_f   ist immer surjektiv.

Die Graphen der eingeschränkten Umkehrfunktionen erhältst du jeweils durch Spiegelung des Graphenteilstücks an der 1. Winkelhalbierenden.

-----

#

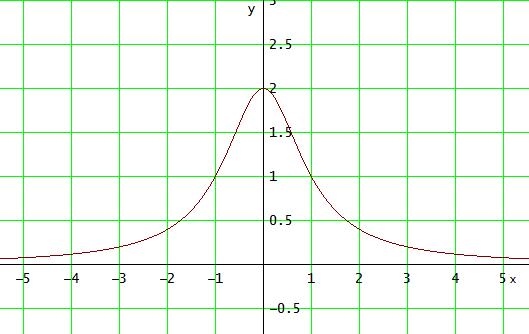
Falls  f(x) =  2 / (x² + 1) gemeint ist, erfolgt die Betrachtung analog:

D_f = [ -3 ; 3 ]  ;  f(±3) = 1/5 

f '(x) = - 4·x / (x² + 1)²

→   Hochpunkt (0|2)  →  W_f = ] 1/5 ; 2 ]   

f '(x) < 0 für x > 0  →  f  streng monoton fallend in [ 0 ; 3 ]

f '(x) > 0 für x < 0  →  f  streng monoton steigend  in [ -3 ; 0 [

Gruß Wolfgang

Comments

Ich habe da nur nochmal eine Frage, wenn ich +/-3 in die Fuktion einsetze um Wf auszurechnen, komme ich auf 12/9? 
ist das jetzt ein Denkfehler von mir oder haben Sie sich verschrieben ? 

---

Für f(x)  =  2/x² + 1

f(3) = 2/3²  + 1 =  2/9 +  9/9 = 11/9

 Für  f(x)  =  2 / (x² + 1) 

f(3) = 2 / (3² + 1) = 2/10 = 1/5 

---

oh, danke, ich habe meinen Denkfehler entdeckt.

ich habe auch gerade gesehen ich muss die dazugehörigen lokalen Umkehrfunktionen angeben ich habe auch schon etwas angefangen aber das sieht so falsch aus. könnten sie mir bei dem Ansatz nur mal held´fen, den Rest sollte ich dann alleine schaffen? 

Answer 2

http://www.math.uni-hamburg.de/teaching/export/tuhh/cm/a1/0607/vorl03_ana.pdf

und die Funktion mal plotten:

www.matheretter.de/rechner/plotlux/

---

Funktion hat wirklich keine Klammern oder doch ? Bitte zweifelsfrei posten - damit zum Beispiel:

www.matheretter.de/rechner/tex/