Bestimme den Definitionsbereich damit die Funktion surjektiv wird und warum sie nicht injektiv ist

Question

Hallo ich habe eine Aufgabe gestellt bekommen die ich bis Montag lösen soll:

EDIT(Lu): Funktion gemäss Kommentar f(x) : = - √(2 - x²)

a) ich soll den maximalen Definitionsbereich D_f   ⊂ ℝ und die Menge W_f   ⊂ ℝ bestimmen damit

f : D_f → W_f  , x ↦ f(x)  eine surjektive Abbildung wird.

b) Ich soll die Frage beantworten ; warum f nicht Injektiv ist

Dabei soll ich die größt möglichen Intervalle I ⊂ D_f  angeben, auf denen die Einschränkung f _I   injektiv ist.

Ich soll außerdem die zugehörigen lokalen Umkehrfunktionen angeben.

Ich habe bis jetzt noch keine Ahnung wie ich da dran gehen soll, ich hoffe ihr könnt mir weiterhelfen

Ich bedanke mich schon mal im voraus !       : )

Comments

Sollst eine Funktion erfinden?

---

ups Funktion ist gegeben

meine Schuld

f(x) = - √2-x²

---

f(x) = - √(2 - x²) , also alles unter der Wurzel?

---

ja genau, hab die klammer vergessen

Answer 1

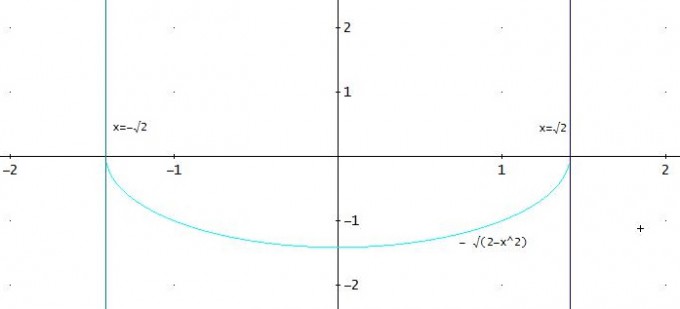
f(x) = - √(2 - x²) 

maximaler Definitionsbereich D_f =  [ - √2 ; √2 ] , denn der Term unter der Wurzel darf nicht negativ sein.

Der minimale Funktionswert ist also 0, der maximale √2 (für x=0)  → W_f = [ 0 ; √2 ]

a)  f:  [ - √2 ; √2 ] → [ 0 ; √2 ] , x ↦  - √(2 - x²)   ist surjektiv.

b)  Bei einer injektiven Funktion müssen verschiedene x-Werte auch verschieden Funktionswerte haben.

f ist nicht injektiv, weil z. b. f(-1) = f(1) = -√1 = -1 übereinstimmen.

 f₁ :  [ - √2 ; 0 ] → [ 0 ; √2 ] , x ↦  - √(2 - x²)   und

 f₂ :  [ 0 ; √2 ] → [ 0 ; √2 ] , x ↦  - √(2 - x²)    sind injektiv 

(f2 ist streng monoton steigend, f1 streng monoton fallend.)

Gruß Wolfgang