Hallo Pia,
Ja - ich sehe das genauso wie Lu. Ich entziffere aus dem Bild
$$g_{h,|\vec{AB}|} \circ g_{h,|\vec{AB}|} \circ g_{h,|\vec{AB}|}$$
Was drei Gleitspiegelungen hintereinander wären. Als Tipp steht da, dass Spiegelung und Verschiebung kommutativ sind. D.h. man kann auch zunächst drei Verschiebungen und anschließend drei Spiegelungen (was identisch mit einer Spiegelung wäre!) ausführen - und das wäre:
$$\space = g_{h,3|\vec{AB}|}$$
das ganze noch mal im Bild, den ein Bild sagt mehr als tausend Worte ;-)
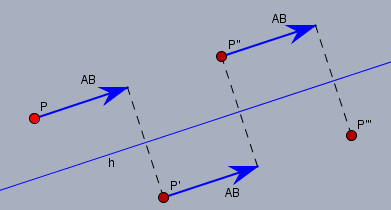
obige Skizze zeigt Dir drei Gleitspiegelungen hinter einander. Der Punkt \(P\) wird auf \(P'\) abgebildet, indem er um den Vektor \(\vec{AB}\) verschoben und anschließend an \(h\) gespiegelt wird. Genauso wird \(P'\) auf \(P''\) und anschließend auf \(P'''\) abgebildet.
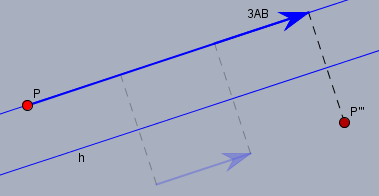
Die selbe Abbildung erhält man, wenn man eine Verschiebung um \(3\vec{AB}\) ausführt und anschließend einmal an \(h\) spiegelt. Zwei Spiegelungen heben sich gegenseitig auf. Das sieht so aus:
Und zum Schluss noch mal als Spiegelrechnung: Eine Gleitspiegelung eines Punktes \(P\) um \(\vec{AB}\) an einer Geraden \(h: \space \vec{n} \vec{x} = d \) mit \(|\vec{n}|=1\) sieht so aus:
$$P' = P + \vec{AB} - 2\left(\vec{n}P -d \right)\vec{n}$$
Wenn Du diese dreimal hintereinander ausführst, so sollte
$$P''' = P + 3\vec{AB} - 2\left(\vec{n}P -d \right)\vec{n}$$heraus kommen.
Gruß Werner