Gleitspiegelung Elemente der Geometrie

Question

Aufgabe:

1. Aufgabe 
a) Zeichnen Sie in ein geeignetes Koordinatensystem...
i. ... das Dreieck mit den Punkten (1| − 1), (4| − 2) und (2| − 2).
ii. ... die Geraden , und , wobei die Gerade auf der y-Achse liegt,die Gerade
durch die Punkte (2|0) und (2|2) verläuft und die Gerade auf der -Achse
liegt.
b) Bilden Sie das Dreieck durch a•b•c ab.
c) Zeigen Sie mithilfe ihrer Zeichnung, dass, a•b•c = a•r mit r=2 x Abstand (b,c) gilt.
und begründen Sie dies kurz in Worten.

Problem/Ansatz:

… Kann mir jemand bei Aufgabe 1b und c) weiterhelfen?

Answer 1

Hallo,

ich rate mal, wie die Aufgabe genau heißt. Meine Vermutung:

a) Zeichnen Sie in ein geeignetes Koordinatensystem...
i. ... das Dreieck mit den Punkten (1| − 1), (4| − 2) und (2| − 2).
ii. ... die Geraden \(a\), \(b\) und \(c\), wobei die Gerade \(c\) auf der Y-Achse liegt,die Gerade \(b\) durch die Punkte (2|0) und (2|2) verläuft und die Gerade \(a\) auf der X-Achse liegt.

b) Bilden Sie das Dreieck durch \(a \circ b \circ c\) ab. 

(Bedeutet: spiegele das Dreieck an \(c\), \(b\) und \(a\) in dieser Reihenfolge)

das sähe dann so aus:

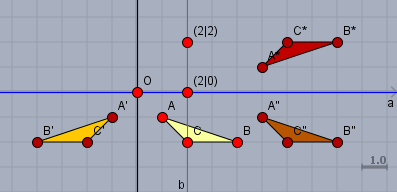
Das Dreieck \(\triangle ABC\) (hellgelb) wird dan der Y-Achse (schwarz) gespiegelt, dann an \(b\) (grün) und schließlich an der X-Achse (blau).

c) Zeigen Sie mithilfe ihrer Zeichnung, dass \(a \circ b \circ c = a \circ r\) mit \(r=\) 2 mal Abstand (b,c) gilt.
und begründen Sie dies kurz in Worten.

Durch die Spiegelung an zwei parallelen Geraden wird das Dreieck \(\triangle ABC\) um den doppelten Abstand dieser Geraden verschoben (Translation). Und anschließend an \(a\) (blau) gespiegelt. Das Resultat ist eine Gleitspiegelung.

Gruß Werner