Bestimmung einer nicht direkt messbaren Entfernung zweier Punkte

Question

es geht um folgende Fragestellung:

Um die nicht direkt messbare Entfernung zweier Punkte P und Q in der Ebene zu bestimmen, steckt man eine 250m lange Standlinie AB ab und misst folgende Horizontalwinkel:

BAP = 102,5°
BAQ = 21,6°
ABP = 37,8°
ABQ = 122,3°

Berechnen Sie die Länge der Strecke PQ!

Wie geht man denn hier vor?

Answer 1

hallo DramaQueen,

mache Dir erst mal eine Zeichnung:

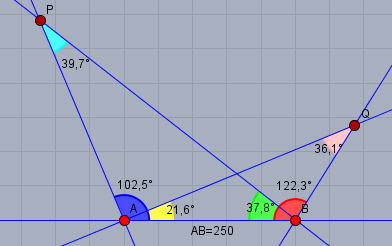
Den hellblauen Winkel bei \(P\) und den rosafarbenen bei \(Q\) kann man über die Winkelsumme im Dreieck berechnen. Dann berechne die Strecke \(PA\) nach dem Sinussatz.

$$\frac{PA}{\sin 37,8°} = \frac{AB}{\sin 39,7°} \quad \Rightarrow PA = AB \frac{\sin 37,8°}{\sin 39,7°}$$

und die Strecke \(AQ\) ebenso

$$\frac{AQ}{\sin 122,3°} = \frac{AB}{\sin 36,1°} \quad \Rightarrow AQ = AB \frac{\sin 122,3°}{\sin 36,1°}$$

Die Strecke \(PQ\) folgt jetzt aus dem Cosinussatz im Dreieck \(AQP\) - es ist

$$PQ^2 = PA^2 + AQ^2 - 2 \cdot PA \cdot AQ \cdot \cos(102,5°- 21,6°)$$

$$\space \Rightarrow PQ \approx 398,7\text{m}$$

Rechne es bitte noch mal nach.

Gruß Werner

Comments

danke für die Rückmeldung. Allerdings weiß ich noch nicht ganz wie du auf die ersten beiden Winkel P und Q kommst? Könntest du mir das genauer erklären?

Danke und Grüße

---

Meine Rückfrage hat sich erledigt! !