Übung Kurvendiskussion. f(x) = x^3 - 6x^2 + 8x

Question

Hi, ich bins nochmal :)

Heute mal bisschen aktiver als sonst, also da kann auch noch mehr kommen. Bereite mich aktuell auf eine Prüfung vor.
Ich habe so eben eine Kurvendiskussion geübt. Kann mir jmd. Das mit überprüfen. 
Das grünmarkierte ist die Gleichung f (x). Ich hoffe das Bild lädt diesmal hoch.

Comments

Die Gleichung \(f^{\prime\prime}(x)=0\) wird nicht mit der \(pq\)-Formel gelöst. Es gibt nur eine Wendestelle.

---

Wichtiger Hinweis von nn! Bei mir liegt dieses Blatt quer auf dem Bildschirm und ich habe den Wendepunkt W einfach vermisst. 

Answer 1

Jedenfalls hast du schon mal ordentlich geschrieben und beschriftet. Dann kommt das normalerweise auch gut. Schreibe noch die Extremwerte an. Punkte kannst du mit 2 Koordinaten angeben. 

Bei Wendepunkten gibt man meist den Punkt explizit W(x_(w) | y_(w)) .

Zur Kontrolle kannst du schon mal

f(x) = x^3 - 6x^2 + 8x (habe ich richtig abgeschrieben?) bei 

https://www.wolframalpha.com/input/?i=f(x)+%3D+x%5E3+-+6x%5E2+%2B+8x eingeben. 

Graph:

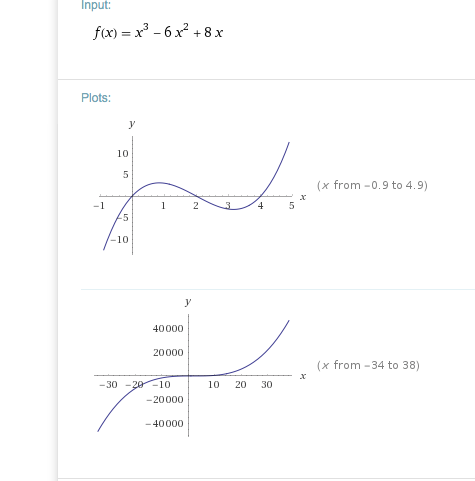
Nullstellen:

Ableitung, Extremstellen und Extremwerte:

Noch auf "Approximation" drücken, wenn du die gerundeten Kommazahlen sehen möchtest. 

Comments

Was wolltest du eigentlich nachher (auf dem zweiten Blatt noch machen)? Die Nullstellen hast du doch schon. 

Dein Rechenweg sieht ganz verkehrt aus. 

---

Da wollte ich dann noch die Schnittpunkte mit den Achsen berechnen. Das ist also falsch? Wie wäre es denn richtig?

---

Die Nullstellen befinden sich dort, wo die Kurve die x-Achse schneidet. 

Schnittpunkte mir der x-Achse sind daher P(0|0) , Q(2|0) und R(4|0).

Den Schnittpunkt mit der y-Achse hast du damit auch schon: P(0|0) . 

Answer 2

Nullstellen und Extremstellen auf dem
ersten Blatt stimmen.
Was bedeuten die 83/40000 ?

2.Blatt :
f ´´ ( x ) = 6x - 12
6x - 12 = 0
x = 2
Nichts mit einer pq-Formel.

Dann kommt noch eine weitere Funktion.
Was wird da gemacht ?