Kurvendiskussion: f(x)=(x^2-4)/(x^2-6x+5)

Question

Könntet Ihr mir bitte helfen diese Aufgabe zu lösen?

Diskutieren Sie die Funktion: 

f(x) = (x² - 4) / (x² - 6x + 5)

-Nullstellen

-Verhalten in einer Umgebung der Nullstellen

-Definitionsbereich, Definitionslücke, eventuell Polen

-Verhalten im Unendlichen, eventuell Asymptote

-Symmetrien(falls vorhanden)

Comments

Steht da nicht noch ein Rechenzeichen zwischen den Brüchen? Bitte schaut doch mal ob ihr wirklich die Angaben in den Aufgaben richtig und vollständig angegeben habt. Ansonsten muß man da ins blaue hinein raten.

Auch das = fehlt hinter dem f(x).

Meinst du eventuell
f(x) = (x^2 - 4) / (x^2 - 6x + 5)

---

Genau so lautet die Aufgabe.Zwischen den Brüchen steht kein Rechenzeichen.

Sorry, dass ich das = Zeichen vergessen habe.

Answer 1

Annahme das die Funktion so lautet, wie der mathecoach es angenommen hat :

Vielleicht hilft das schon mal weiter.

Answer 2

f(x) = (x² - 4) / (x² - 6x + 5) 

-Nullstellen

Ein Bruch wird null wenn der Zähler null wird. 
x^2 - 4 = 0
x = ± 2

-Verhalten in einer Umgebung der Nullstellen

lim x → 2^- (x² - 4) / (x² - 6x + 5) = 0⁺
lim x → 2⁺ (x² - 4) / (x² - 6x + 5) = 0^-

lim x → -2^- (x² - 4) / (x² - 6x + 5) = 0⁺
lim x → -2⁺ (x² - 4) / (x² - 6x + 5) = 0^-

-Definitionsbereich, Definitionslücke, eventuell Polen

Man untersucht den Nenner auf Nullstellen
x^2 - 6x + 5 = 0
x = 5 ∨ x = 1

Definitionsbereich D = R \ {1, 5}

-Verhalten im Unendlichen, eventuell Asymptote

Polynomdivision ergibt 1 plus irgendein Restterm. Also ist die Asymptote y = 1 

-Symmetrien(falls vorhanden)

Keine Symmetrie

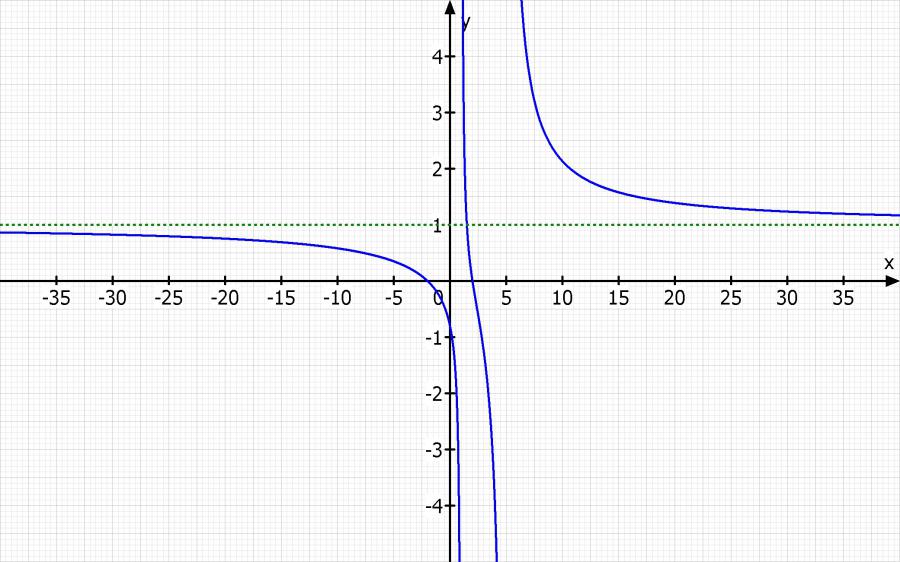
Skizze: