Partialbruchzerlegung reell und komplex

Question

Bestimmen Sie die reelle und komplexe Partialbruchzerlegung von: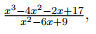

Als erstes habe ich, da der obere Teil einen höheren Grad hat, oben durch unten geteilt. (polynomdivision) und bin auf x+2. und rest x-1 gekommen. und den unteren Teil mithilfe der 2. binomischen formel zu (x-3)^2 geformt.

somit bin ich auf x-1/x-3^2 = A/x-3 + B/(x-3)^2 gekommen. nun würde ich eine multiplikation mit dem nenner durchführen und komme auf x-1=A(x-3)+B(x-3)^2.

Wir haben es so gelernt, nun jeweils den A- und B-wert auf 0 zu bekommen. also x=3

Nun verschwinden meine beiden Werte(A,B) aber ?

Wo liegt der fehler

Answer 1

somit bin ich auf (x-1)/(x-3)² = A/(x-3) + B/(x-3)² gekommen. 

->das stimmt.

->mal Nenner

x-1=A(x-3) +B

----< 1=A 

B=2

Comments

x-1=A(x-3) +B

----< 1=A

B=2

B=2 erhält man wenn man 3 einsetzt oder?

kannst du das nochmal erläutern, wie du auf A=1 kommst?

---

ich hab das mit dem Koeffizientenvergleich gemacht:

x-1=A(x-3) +B

x-1=Ax -3A +B

x^1: 1 =A

x^0: -1= -3A+B

-----------------

-1= -3 +B

B=2