Hallo Queenie,
grafische Lösung im Maßstab 1 : 1000
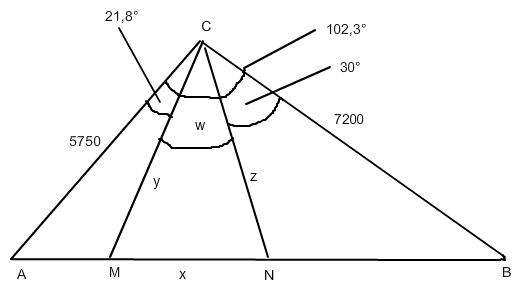
Zeichne AC mit Länge b = 5750 mm = 5,75 cm
Trage in C an CA den Winkel γ = 102,3° an.
Im Folgenden sind benötigte Punkte nacheinander durch zwei Ortslinien festgelegt, deren Schnittpunkt jeweils der gesuchte Punkt ist
B liegt
1) freier Schenkel von γ
2) Kreis um C mit r = a = 7200 mm = 7,2 cm
Verbinde A mit B
M liegt
1) Strecke AB
2) freier Schenkel von Winkel 21,8° angetragen in C an CA
N liegt
1) Strecke AB
2) freier Schenkel von Winkel 30° angetragen in C an CB
Aber wo lege ich denn optimalerweise das Geodreieck an

Rechnung:
Im ΔABC kannst du mit dem Kosinussatz aus a = 7200 , b = 5750 und γ = 102,3° die Strecke BC = c = 10126,27
und dann mit dem Sinussatz α = 44° und β = 33,7° berechnen.
In den Dreiecken ΔAMC und BCN kann man dann jeweils den dritten Winkel und mit dem Sinussatz die Seiten y = 4379,12 und z = 4456,15 ausrechnen.
In ΔMNC ergibt sich Winkel w = 102,3° - 21,8° - 30° = 50,5°
Aus y, z und Winkel w ergibt sich dann mit dem Kosinussatz die Länge
x = 3769,49 von Strecke MN.
Gruß Wolfgang
------
Der Winkel BCN ist in der Aufgabenstellung falsch bezeichnet, es müsste NCB heißen