Ich habe mir alles noch einmal überlegt.
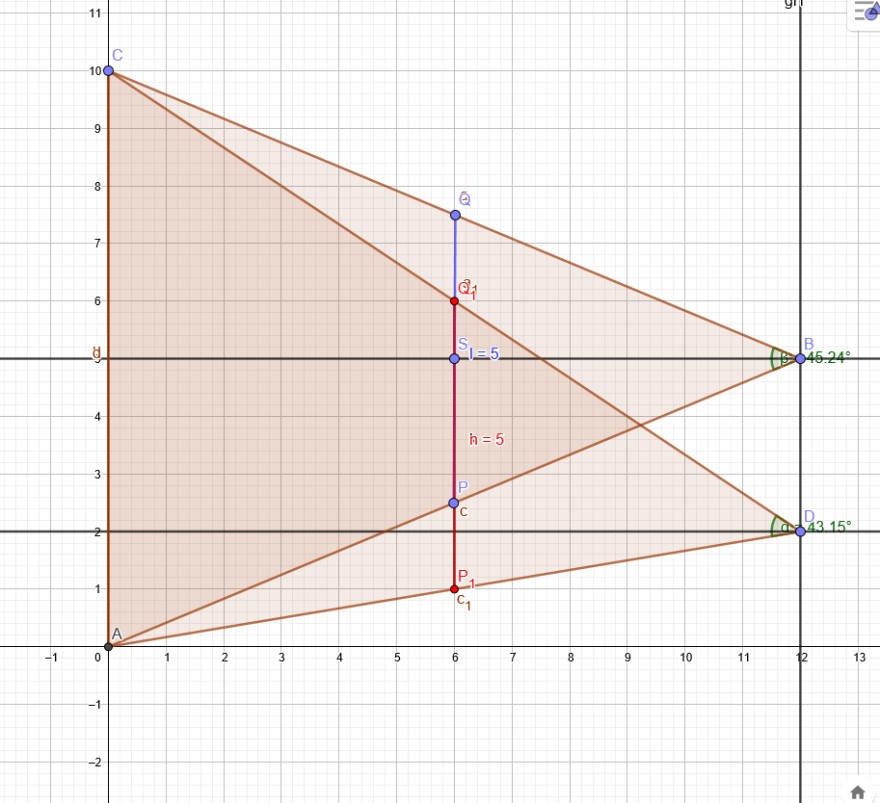
"Gast hj2166" hat Recht gehabt. Es gibt "unendlich" viele Dreiecke, wo \(\frac{BP}{BA} =\frac{BQ}{BC}=\frac{3}{6}=\frac{1}{2}\) gilt.
Die Strecke PQ ist immer gleich 5. Die Strecken c und a sind unterschiedlich.
Der Flächeninhalt ist immer \(A=\frac{10*12}{2}cm^{2} \) groß.
In der Aufgabenstellung würde etwa eine Winkelangabe für Eindeutigkeit sorgen.