Hallo Peter,
-1 und -2 sind die Nullstellen von x2+3x+2 = (x+1) * (x+2) und damit von f.
Wegen f(x) ≥ 0 sind das globale Minimumstellen von f.
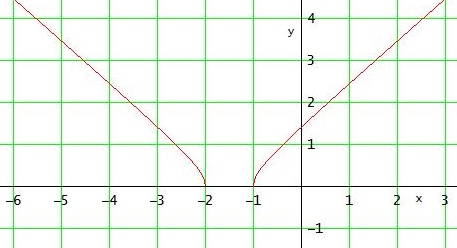
f(x)= √(x2+3x+2) D = ] - ∞ ; -2 ] ∪ [ -1 ; ∞ [ wegen x2+3x+2 ≥ 0
f '(x) = (2·x + 3) / (2·√(x2 + 3·x + 2)) hat keine Nullstelle ( -3/2 ∉ D )
f '(x) > 0 in ] -1 ; ∞ [ → f streng monoton steigend in ] - 1 ; ∞ ]
f '(x) < 0 in ] - ∞ ; - 2 ] → f streng monoton fallend in ] - ∞ ; -2 ]
→ Es gibt sonst keine Extrema.
Gruß Wolfgang