Berechnungen an Körpern. Trigonometrie. Regelmässiges Oktaeder

Question

Liebe Leute, könntet ihr mir bitte bei dieser Aufgabe helfen? Komme bei dieser Aufgabe überhaupt nicht weiter... benötige ich nicht die Länge der Seite a? Bei der Angabe steht diesbezüglich aber nichts... Lt. Lösungsheft kommt für Alpha ca. 109,5 Grad heraus... ..

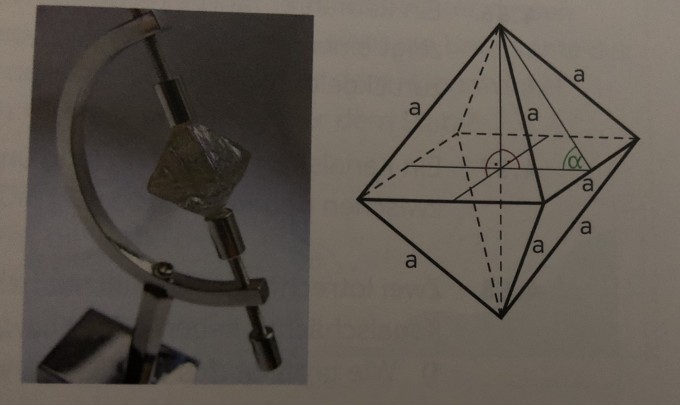
Diamanten kristallisieren am häufigsten in der Form eines regemäßigen Oktaeders, einer achtseitigen Doppelpyramide mit lauter gleich langen Kanten. Unter welchem Winkel Alpha sind schneidende Seitenflächen gegeneinander geneigt?

Answer 1

(a/2)^2 + (a/2)^2 + h^2 = a^2 --> h = √2/2·a

tan(α) = h / (a/2) --> α = arctan(2·h/a) = arctan(2·(√2/2·a)/a) = 54.74°

Du findest alles über den Oktaeder auf

http://www.mathematische-basteleien.de/oktaeder.htm

Comments

Vielen vielen Dank, hast mir sehr damit geholfen ...;)))

Answer 2

Du brauchst zunächst h_(a). Das ist die Höhe der Seitenflächen.

h_(a)=√(a^2-a^2/4)=√3/2*a

α=arccos(a/(2*h_(a)))=arccos(2a/(2*√3*a)=arccos(1/√3)=54,74°

Damit ist der gesuchte Winkel=2*α=109,47°

Comments

Vielen vielen Dank..;)) habe es verstanden ;)) 

---

Nur eines noch, warum muss ich am Ende 2x Alpha rechnen?

---

Der Winkel alpha ist in der Aufgabe falsch eingezeichnet. Er markiert den Winkel zwischen der Pyramidenseite und der Grundfläche. Man soll laut Aufgabe aber den Winkel bestimmen, den die sich schneidenden Seiten des oktaeders einschließen. Dieser ist doppelt so groß wie alpha.

---

Ah okay verstehe, das heißt, der grüne winkelbogen müsste in der Zeichnung noch einmal weiter nach unten verlaufen stimmt‘s?

---

Absolut richtig!!! Deswegen kriegt auch der mathecoach für alpha nur den halben Winkel raus.

---

Beziehungsweise müsste der grüne Winkelbogen bei der mit a bezeichneten schwarzen Kante aufhören, also nach unten weiter verlaufen und bei der schwarzen dicken Kante aufhören?

---

Nein, er müsste nicht bis zur schwarzen dicken kante gehen sondern bis zur einer dünnen scharzen linie die es in dem unteren Dreieck geben müsste, die aber nicht eingezeichnet wurde. 

---

Das bedeutet, dass nach unten hin eigentlich auch noch ein Dreieck eingezeichnet sein müsste?

---

Ja genau, um den Winkel richtig einzeichnen zu können, müsste in dem unteren Dreieck auch die Seitenhöhe eingezeichnet werden, wie bei dem oberen Dreieck, wo der Winkel anfängt.

---

Du meinst eine dünne schwarze Linie, die Eine einem nach unten eingezeichneten (fehlenden) rechtwinkeligen Dreieck zugehörig wäre?

---

Ja ganz genau.

---

Okay, nochmals vielen vielen Dank!!! Du warst mir eine riesengroße Hilfe!!!

---

Ganz prima. Ich finde es gut dass du solange fragst, bis du es verstanden hast.