Funktionen. Umkehrfunktion bestimmen

Question

Wie kann ich bei dieser Aufgabe die Umkehrfunktion bestimmen? 

Gibt es dafür einen bestimmen Ansatz den man verwenden kann? Also Regel oder so...

 

in der Aufgabe steht ja "unter Einschränkung des Definitionsbereichs". Wie wäre es denn z.B wenn dieser Satz nicht vorhanden wäre, sondern nur stehen würde "bestimme die Umkehrfunktion" ? 

Ist diese Umkehrfunktion immer von etwas Abhängig ; Definitionsbereicht, Wertebreich etc...??

Answer 1

Du musst nur nach x auflösen

y = 1/2·x + 2 --> x = 2·y - 4

y = (1 - x)/(1 + x) --> x = (1 - y)/(1 + y)

Danach wäre noch x und y zu vertauschen. Aber das solltest du auch hinbekommen denke ich.

Comments

y = x^2 mit D = [0 ; ∞]

und 

y = √x mit D = [0 ; ∞]

sind Umkehrfunktionen

----------

y = x^2 mit D = ]-∞ ; 0] 

und 

y = -√x mit D = [0 ; ∞]

sind Umkehrfunktionen

Skizziere die zu den Funktionen mal den Graphen. Was fällt dir auf.

Answer 2

a) y= 1/2*x+2

Nach x auflösen:

y-2= 1/2*x

x= 2y-4

Vertauschen:

f^{-1}= y =2x-4

b) y = (1-x)/(1+x)

y(1+x) = 1-x

y+xy+x=1

x(y+1) = 1-y

x= (1-y)/(y+1)

f^{-1} = (1-x)/(x+1)

Funktion und Umkehrfkt. fallen zusammen.

Answer 3

Zu Defintionsbereich und Wertebereich

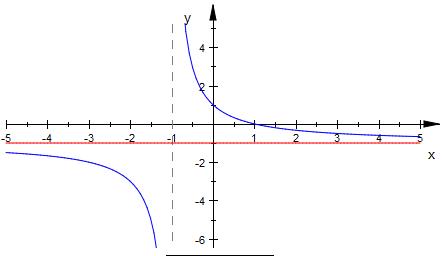
y = (1-x)/(1+x)
Division durch 0 ausschließen
D =ℝ \ { -1 }

Wertebereich
untersuchen : x gegen ∞,  -1 ( - ) -1 ( +), -∞

lim x −> - ∞ [  ( 1 - x ) / ( 1 + x ) ] = +∞ / -∞ = -1(-)
lim x −> - 1 (-)  [  ( 1 - x ) / ( 1 + x ) ] = 2(-)  / 0(-) = -∞
lim x −> - 1 (+)  [  ( 1 - x ) / ( 1 + x ) ] = 2(+)  / 0(+) = +∞
lim x −> ∞ [  ( 1 - x ) / ( 1 + x ) ] = -∞ / +∞ = -1 (+)

W = ℝ \ { -1 }

Es gilt

Der Definitionsbereich der Funktion ist gleich dem
Wertebreich der Umkehrfunktion.
Der Wertebereich der Funktion ist gleich dem
Definitionsbreich der Umkehrfunktion.

Def-und Wertebereich der Funktion sind gleich.
Dies gilt auch für die Umkehrfunktion.