Asymptote einer Funktion ermitteln f(x)=x^2+3*x+6/-5*x^3+5*x^2-8*x-7

Question

Gegebene Funktion f(x)=x^2+3*x+6/-5*x^3+5*x^2-8*x-7

Ermitteln für x->+- unendlich

Comments

https://www.matheretter.de/wiki/bruch-schreiben

---

Kürze mit x^3.

---

f ( x ) = x^2+3*x+6/-5*x^3+5*x^2-8*x-7 

bei dir steht

f ( x ) = x^2+3*x+ (6/-5*x^3)+5*x^2-8*x-7

du meinst aber

f ( x ) = ( x^2+3*x+6 ) / (-5*x^3+5*x^2-8*x-7 )

Bei dir fehlen die Klammern.

Answer 1

da die höchste Potenz im Zähler kleiner als die höchste Potenz im Nenner ist gibt es folgendes:

$$ \lim_{x\to\pm\infty}\frac{x^2+3x+6}{-5x^3+5x^2-8x-7}=0 $$

Answer 2

lim x−> ±∞  [ ( x^2+3*x+6 ) / (-5*x^3+5*x^2-8*x-7 ) ]

am stärksten wachsen die höchsten Potenzen,
alles andere spielt keine Rolle mehr und kann entfallen.

lim x−> ±∞  [ x^2/  (-5 * x^3 ) ] | x^2 kürzen

lim x−> ±∞  [ 1 /  (-5 * x ) ]  = 1 / ± ∞

lim x−> ±∞  = 0

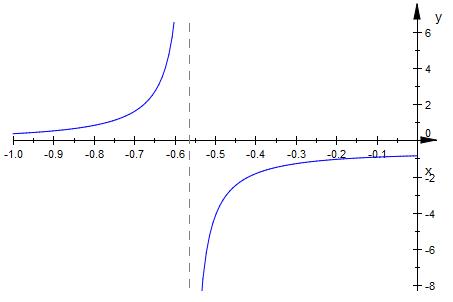
Die horizontale Asymptote ist y = 0.

Der Nenner wird bei x = 0.564 zu null.
Dies ergibt eine Polstelle.
Die vertikale Asymptote ist x = 0.564

Comments

Hallo Georg,

> ... alles andere spielt keine Rolle mehr und kann entfallen.

Das gilt im Allgemeinen für die Grenzwerte  mit x → ± ∞ , nicht aber für die Asymptote im Unendlichen.