Verktorrechnung Mach aus Dreieck Parallelogramm

Question

Hallo ich habe da ein Problem mit einer Aufgabe

DIe Punkte A(3/2/1) b(-1/4/2) und C(-3/1/3) bilden ein Dreieck.

Bestimmen sie die Koordinaten eines Punktes D so,dass ABCD ein Parallelogramm ist.

Weiß absolut nicht wie ich an diese Aufgabe rangehen soll.

Answer 1

Nun, dazu gibt es mehrere Möglichkeiten. Schau mal auf mein Bild, dort ist eine solche Möglichkeit gezeigt.

Gegeben ist das Dreieck ABC, gesucht der Punkt D, sodass ABCD ein Parallelogramm ist.

 

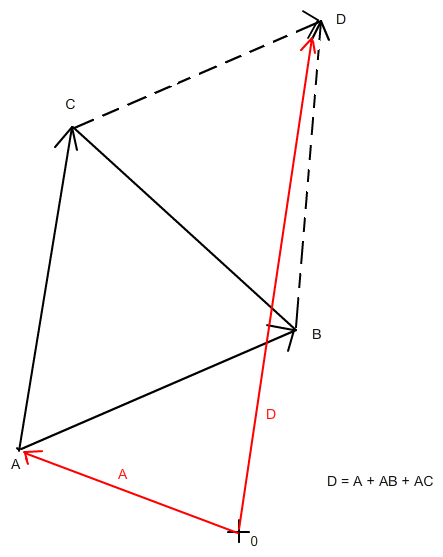
Also:

D = A + AB + AC

= A + ( B - A ) + ( C - A )

= B + C - A

= ( -1 / 4 / 2 ) + ( - 3 / 1 / 3 ) - ( 3 / 2 / 1 )

= ( - 7 / 3 / 4 )

 

Zur Probe, ob ABCD tatsächlich ein Parallelogramm ist, prüfe, ob gilt:

AB = CD und AC = BD

Wenn beides gilt, dann ist ABCD ein Parallelogramm.

AB = CD <=> B - A = D - C

<=> ( - 1 / 4 / 2 ) - ( 3 / 2 / 1 ) = ( - 7 / 3 / 4 ) - ( - 3 / 1 / 3 ) 

<=> ( - 4 / 2 / 1 ) = ( - 4 / 2 / 1 )

Die beiden Vektoren AB und CD sind gleich.

AC = BD  <=> C - A = D - B

<=> ( - 3 / 1 / 3 ) - ( 3 / 2 / 1 ) = ( - 7 / 3 / 4 ) - ( - 1 / 4 / 2 )

<=> ( - 6 / - 1 / 2 ) = ( - 6 / - 1 / 2 )

Auch die Vektoren AC und BD sind gleich.

Also ist ABCD tatsächlich ein Parallelogramm.

Comments

Vielen Dank schonmal.

Jetzt habe ich den Sachverhalt schon einmal verstanden.

Gesucht ist also ein punkt D der so liegen soll das ein Parallelogramm entsteht.

--> D gesuchte größe

Aber so ganz versteh ich den Weg nicht wie du dort hinkommst.

Wieso ergibt A (Was ist A? der Punkt der gegeben ist?) + AB+AC die gesuchte Strecke?

Und wenn du von Strecke AB redest meinst du sicherlich den Vektor AB? Also den berechnet man ja wie du schon geschrieben hast End-Anfangspunkt.

Den Rest der rklärung habe ich verstanden also das die Strecken der Seiten gleich sein müssen aufgrund der eigenschaften eines Parallelogramms.

Danke für deine Mühe.

---

Und wenn du von Strecke AB redest meinst du sicherlich den Vektor AB?

Das Wort "Strecke" habe ich nicht benutzt ... AB, AC sollen aber natürlich Vektoren sein.

 

Wieso ergibt A (Was ist A? der Punkt der gegeben ist?) + AB+AC die gesuchte Strecke?

Es ist keine Strecke gesucht, sondern ein Punkt, nämlich der Punkt D, in Koordinatendarstellung. Diese geht vom Ursprung aus. Ich muss also einen Vektorzug finden, der vom Ursprung O ausgeht, nur aus den bekannten Vektoren besteht und zum Punkt D führt. Ein solcher Streckenzug ist

OA , AB , AC

(wobei ich OA durch A abgekürzt habe und der Vektor AC natürlich im Punkt B angelegt werden muss)

 

Übrigens: Es gibt eine schönere Lösung, bei der der Punkt D so berechnet wird, dass die Eckpunkte des Parallelogramms dann auch in mathematisch korrekter Reihenfolge (alphabetisch aufsteigend entgegen dem Uhrzeigersinn) bezeichnet sind. Vielleicht kannst du ja mal versuchen, DIESEN Punkt D zu finden ...