Konstruktion von Dreiecken, Studium

Question

Hallo kann mir einer hier eventuell weiterhelfen ? Ich verstehe es leider noch nicht . Muss auch nicht unbedingt Geogebra sein, es würde mir schon reichen wenn es jemand aufzeichnet, vielleicht verstehe ich es dann ja schon .

Answer 1

Hallo lia,

ein beliebiges Dreieck zu zeichnen, sollte kein Problem sein. Dann zeichnet man zwei Winkelhalbierende (die gelben Geraden) der Innnewinkel z.B. durch die Punkten \(A\) und \(B\), die sich im Mittelpunkt \(I\) des Inkreises schneiden. Den Inkreis konstruiert man, indem durch den Mittelpunkt \(I\) eine Senkrechte zu einer der Seiten - z.B. \(c\) - konstruiert, die \(c\) im Punkt \(F\) schneidet. Der Radius des Inkreises ist dann \(IF\).

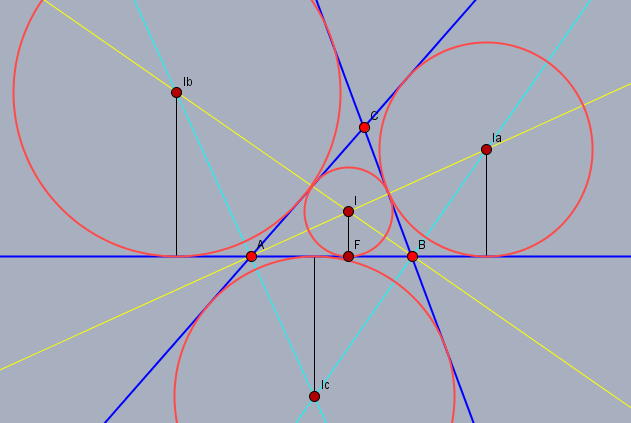
Dann konstruiert man ebenfalls wieder in zwei Punkten die Winkelhalbierenden zu den Außenwinkeln (die hellblauen Geraden) . Tipp: diese stehen immer senkrecht auf den Winkelhalbierenden der Innenwinkel. Diese schneiden sich in \(I_C\) und die Winkelhalbierenden der Innenwinkel in \(I_A\) und \(I_B\). Die Ankreises konstruiert man in der selben Art und Weise wie den Inkreis, indem man vom Mittelpunkt aus, das Lot (schwarze Strecke) auf eine der Seiten fällt.

Wenn Du noch Fragen hast - z.B. zum Aufgabenpunkt b) , so melde Dich bitte.

Gruß Werner

Comments

Danke, ja ich weiß nicht warum sie sich denn jetzt berühren ?:) Danke für deine Mühen.

---

zu b):

jeder Punkt auf einer Winkelhalbierenden ist von den beiden Schenkeln des Winkels gleich weit entfernt (s.a. https://www.mathelounge.de/506226/winkelhalbierenden-schenkeln-winkels-denselben-abstand). D.h. wenn man einen Kreis mit Mittelpunkt auf der Winkelhalbierenden zeichnet, der den einen Schenkel berührt, so muss er auch den zweiten Schenkel berühren.

Der Mittelpunkt der Ankreise liegt nun sowohl auf der Winkelhalbierenden eines Inkreises (gelbe Gerade) als auch auf der Winkelhalbierenden eines Außenwinkels (hellblaue Geraden).

Betrachte dazu den Ankreis um \(I_A\). Er berührt, die Gerade \(c\) durch \(AB\). Dann muss er auch die Gerade \(a\) durch \(BC\) berühren, da \(I_A\) auf der Winkelhalbierenden (hellblau) des Außenwinkels durch \(B\) liegt. Die Schenkel des relevanten Winkels sind hier \(c\) und \(a\). Und genauso muss er die Seite \(b\) durch \(CA\) berühren, da \(I_A\) auf der Winkelhalbiereden (gelb) mit den Schenkeln \(c\) und \(b\) liegt.

Answer 2

In-n-Out Kreise.ggb (14 kb)