f(x):= -2,5x + 16/100x2
1-2 ist gelöst. Jedoch 3 verstehen wir überhaubt nicht.
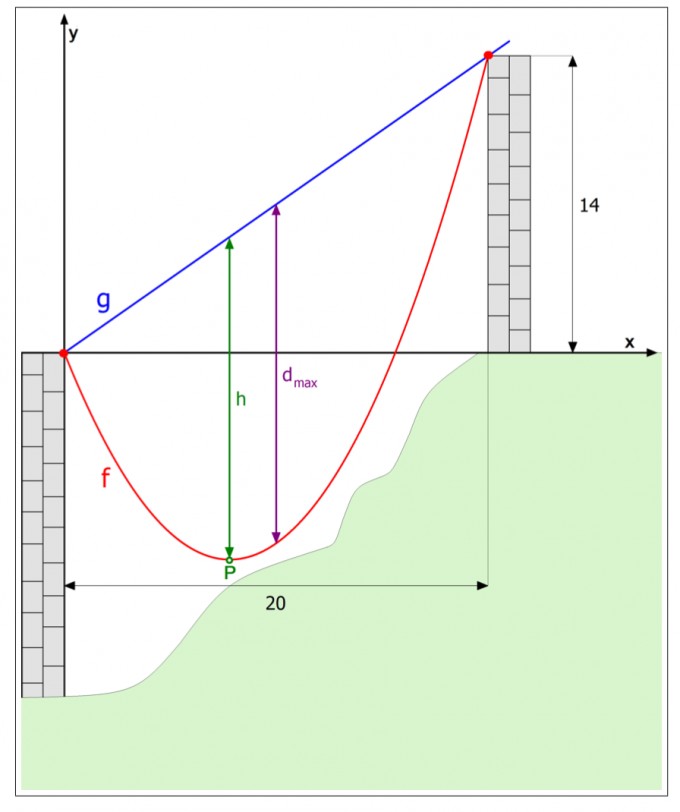
(1) die Länge der Strecke h, wobei der Punkt P den Tiefpunkt der Funktion f de niert und
(2) die Länge des maximalen Durchhangs dmax (siehe Abbildung).
(3) In der nachstehenden Abbildung wird die Hochspannungsfernleitung durch eine Parabel appro- ximiert . Durch welche mathematische Funktion wird ein entsprechendes Seil unter Eigengewicht im Normalfall modelliert?
Aufgabe 1-2
f (x):= -2,5x + 16/100*x2
g ( x ) = 14 / 20 * x
Tiefster Punkt bei
f ´( x ) = - 2.5 + 16/100 * 2 * x
- 2.5 + 16/100 * 2 * x = 0
x = 7.8125 m
f ( 7.8125 ) = - 9.76
g ( 7.8125 ) = 5.47
d = 9.76 + 5.47 = 15.23 m
---------------------------------
dm ( x ) = g ( x ) - f ( x ) =
14/60 * x - ( -2,5x + 16/100*x2 )
3.2 * x - 4/25 x2
dm ´ ( x ) = 3,2 - 8/25 * x
3,2 - 8/25 * x = 0
x = 10 m
dm ( 10 ) = 16 m