Mach erst mal quadratische Ergänzung und schaue dann, was du hast.
a) x^{2} -2x+y^{2} +4y- 20 = 0
(x^2 - 2x +1 ) + (y^2 + 4y + 4) = 20 + 1 + 4
(x - 1)^2 + (y+2)^2 = 25
Kreis mit Mittelpunkt M(1|2) und Radius √(25) = 5
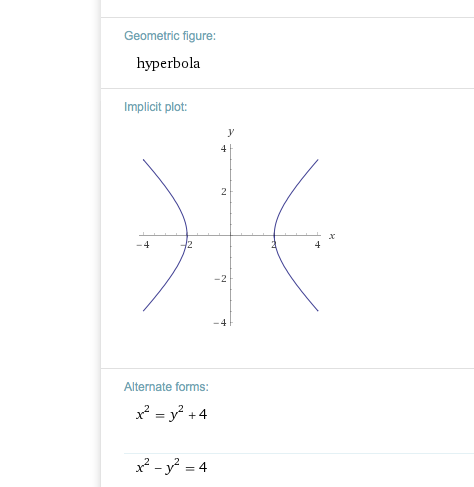
b) x^{2} -y^{2} -4= 0
(x-0)^2 - (y-0)^2 = 4
---> Form erkennen: Hyperbel
Kontrolle mit
https://www.wolframalpha.com/input/?i=x%5E(2)+-y%5E(2)+-4%3D+0
c) 9x^{2} +16y^{2} -18x = 135
x^2 - 2x + 16/9 y^2 = 15
x^2 - 2x + 1 + 16/9 y^2 = 15 + 1
(x-1)^2 + 16/9 y^2 = 16
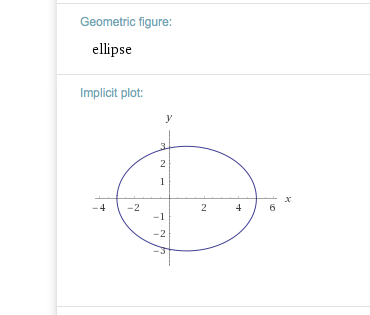
---> Müsste eine Ellipse sein mit Zentrum Z(-1|0). Oder?
https://www.wolframalpha.com/input/?i=9x%5E(2)+%2B16y%5E(2)+-18x+%3D+135
d) y^{2} +2x = 4y
y^2 - 4y = - 2x
y^2 - 4y + 4 - 4 = - 2x
(y-2)^2 - 4 = -2x
-1/2 (y-2)^2 + 2 = x
Parabel ! Allerdings liegend und nach links geöffnet. (x-und y-Achse sind vertauscht!)
Scheitelpunkt hat Koordinaten y=2 und x = 2
Laut meinem Buch steht folgendes
Kreis: A=B
Ellipse: A*B > 0 , A≠B
Hyperbel: A*B <0
Parabel: A=0 , B≠0 oder B=0 und A≠0
A und B musst du der Grundform der Kegelschnittgleichungen entnehmen. Die steht in deinem Buch. Die gegebenen Gleichungen dann auf die vorgegebene Form bringen.
