Herleitung von bedingungen

Question

der graph einer ganzrationalen funktion 4 Grades verläuft durch den punkt P-2 -4  und besitzt im ursprung des koordinatensystem ein relatives minimum der graph besitzt eine nullstelle x -1 wo seine steigung 3 beträgt

Answer 1

Hallo okpio,

f(x) = ax^4 + bx^3 + cx^2 + dx + e

f '(x) = 4·a·x^3 + 3·b·x^2 + 2·c·x + d

Graph geht durch Ursprung:

f(0) = 0 = e  

→  f(x) = ax^4 + bx^3 + cx^2 + dx

f hat im Ursprung ein Minimum:

f '(0) = 0 = →  f(x) = ax^4 + bx^3 + cx^2 

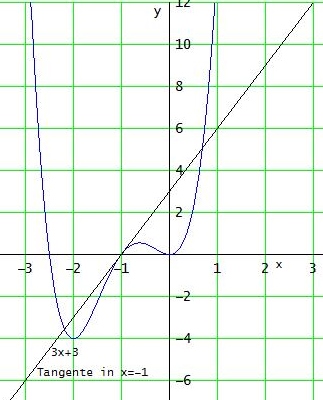
f geht durch P(-2|-4): 

f(-2) = - 4 = 16·a - 8·b + 4·c   (I)  

Nullstelle x = -1:

f(-1) = 0 = a - b + c   (II)

Steigung 3  bei x = - 1 

f '(-1) =  3 = - 4·a + 3·b - 2·c    (III)

LGS  lösen  ergibt   a = 2  ;  b = 7  ;  c = 5

f(x) = 2·x^4 + 7·x^3 + 5·x^2

Gruß Wolfgang

Answer 2

der graph einer ganzrationalen funktion 4 Grades

f ( x) = a*x^4 + b * x^3 + c ^ x^2 + d x + e

verläuft durch den punkt P-2 -4 

f ( -2 ) = -4

und besitzt im ursprung des koordinatensystem

f ( 0 ) = 0

ein relatives minimum

f ´( 0 ) = 0

der graph besitzt eine nullstelle x -1

f ( -1 ) = 0

wo seine steigung 3 beträgt

f ´( -1 ) = 3

Comments

So dann zeig einmal an einem Beispiel ob
du das einsetzen verstanden hast

f ( x ) = a*x^4 + b * x^3 + c ^ x^^2 + d * x + e
f ( -1 ) = 0