Extremwertaufgaben - aus kreisrundem Blech Pyramide mit maximalem Volumen

Question

 Meine Frage:
Aus einem kreisrunden Blech mit 80 cm Durchmesser soll eine quadratische Pyramide mit möglichst großem Volumen geschnitten werden. Bestimmen Sie näherungsweise deren Oberfläche.

Meine Ideen:
Ansatz:

Fläche Kreisblech: r²*π
Oberfläche Pyramide: a² + 2*a*h
Volumen Pyramide: 1/3 a² *h

80 cm = 2*h*a

Wie verbinde ich das nun, um eine Haupt- und Nebenbedingung aufzustellen, die ich benötige, um den Extremwert zu berechnen?

Answer 1

EDIT(Lu): Ursprünglichen Kommentar mit Diskussion in Antwort umgewandelt, da schöne Überlegungen und Formeln! 

Hallo Dumat,

auf welche Weise sollen denn die eine Grund- und vier Seitenflächen aus dem Kreis geschnitten werden? Einfallslos wie hier:

oder mit etwas mehr Phantasie wie hier:

oder kann man das Metall auch einschmelzen und neu walzen?

Gruß Werner

Comments

Hallo Werner,
ich vermute " einfallslos wie hier ". Grins.

---

Hallo Werner,

es soll einfallslos geschnitten werden

---

Hallo Werner-Salomon

Mit welchem Programm hast du die Skizzen gemacht und wie aufwendig ist das für die 2. Zeichnung. 

Ich hätte bei der 2. Bedingung ja schon Schwierigkeiten recht einfach eine Nebenbedingung nu notieren.

---

die Skizzen machen ich i.A. mit Cinderella. Da ich viel Übung habe, geht das recht fix - für eine der obigen Skizzen keine 5min.

Diese 2.Figur muss man IMHO gar nicht optimieren. Man konstruiert aus einem Radius die Diagonale \(MA\) eines Quadrats.

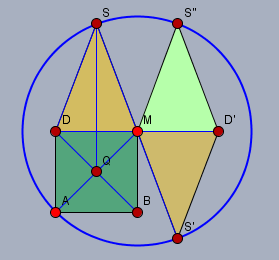
Die Senkrechte zur Seite \(DM\) durch den Mittelpunkt \(Q\) des Quadrats schneidet den Kreis in \(S\). Die weiteren Punkte \(S'\), \(S''\) und \(D'\) ergeben sich aus der Symmetrie. Das Volumen \(V\) der Pyramide ist

$$V=\frac{r^3}{12}\sqrt{3} \approx 9240 \text{cm}^3$$

und damit mehr als 1,5mal so groß wie das 'Optimum', welches in der Aufgabe gesucht war.

Gruß Werner

Edit: Volumen korrigiert

---

mehr als 4mal so groß

Nun übertreib' mal nicht.

---

... kam mir auch ein wenig viel vor. ich hatte das Ergebnis vom Mathecoach übernommen:

$$\frac{\frac14 \sqrt{3}}{\frac{16}{375}\cdot \sqrt{5}} \approx 4,5$$ stimmt das nicht?

---

Ich habe  25·√15 / 64  ≈  1,51

---

Ja mei, da habe ich doch glatt den Faktor 1/3 bei meinem Volumen vergessen. Kannst'e mir aber auch gleich sagen!

---

Das folgende Design ist übrigens noch besser :

---

.. ich wusste doch, das Dir dazu noch was einfällt!

sehr gut!

Answer 2

Achtung: Ungeprüfte Idee

a: Kantenlänge der Grundseite
h: Seitenhöhe
k: Körperhöhe

Nebenbedingung
r = a/2 + h --> a/2 = r - h --> a = 2·(r - h)
Körperhöhe
k^2 + (a/2)^2 = h^2
k^2 + (r - h)^2 = h^2 --> k = √(2·h·r - r^2)

Volumen (Hauptbedingung)
V = 1/3·a^2·k = 1/3·(2·(r - h))^2·√(2·h·r - r^2)
V² = 1/9·(2·(r - h))^4·(2·h·r - r^2) = 16/9·r·(2·h^5 - 9·h^4·r + 16·h^3·r^2 - 14·h^2·r^3 + 6·h·r^4 - r^5)
V²' = 32/9·r·(5·h^4 - 18·h^3·r + 24·h^2·r^2 - 14·h·r^3 + 3·r^4) = 32/9·r·(h - r)^3·(5·h - 3·r)

Maximum
V²' = 0
32/9·r·(h - r)^3·(5·h - 3·r) = 0
5·h - 3·r = 0 --> h = 3/5·r = 0.6·r
a = 2·(r - h) = 2·(r - 0.6·r) = 0.8·r
k = √(2·h·r - r^2) = √(2·0.6·r·r - r^2) = √5/5·r = 0.4472·r
V = 1/3·a^2·k = 1/3·(0.8·r)^2·√5/5·r = 16/375·√5·r^3 = 0.09541·r^3

Oberfläche
O = a^2 + 2·a·h = (0.8·r)^2 + 2·(0.8·r)·(0.6·r) = 8/5·r^2 = 1.6·r^2

Comments

Hallo coach,
was hast du an Volumen herausbekommen.
V = 874.666 cm^3 ?

---

du hast unten in deiner Lösung a = 32 cm und damit Als Grundfläche bereits

a^2 = 1024 cm²

a = 32 cm kann ich über meine Lösung bestätigen wenn du nachschaust.

Answer 3

Volumen Pyramide: 1/3 a^2 *h

80 cm = 2*h*a
a = 40 / h

V ( h ) = 1/3 * ( 40 / h ) ^2 * h
V ( h ) = ( 1600 / 3 )  / h
V ´( h ) = - 1600 / ( 3 h^2 )

- 1600 / ( 3 h^2 ) = 0

Kkeine Lösung. Es gibt kein Maximum.

Comments

Alles falsch.
Die Seitenhöhe muß noch  in die
Körperhöhe umgerechnet werden.

---

Hier die Skizze für den Sachverhalt

 

Hier die Berechnung

a = 32
Das Ergebnis stimmt numerisch.
Ich kann alles auch nochmals etwas
schöner schreiben.

---

Ich denke anhand dessen kann ich die Rechnung nachvollziehen.

---

Nun muss ich doch noch etwas nachfragen.

Wie vollziehen sie den Rechenschritt von V´ zu 2a(1600-40a)-20 a^2?

Bei der Auflösung von V´nach a scheitere ich.

---

Nun muss ich doch noch etwas nachfragen.
Dazu ist das Forum da.

Bitte nachfragen bis alle Klarheiten
beseitigt sind.

---

a = 32
s = 24
h = 17.89
V = 6106 cm^3

O =  a^2 + 4 * ( a*s/2)
O = 2560 cm^2