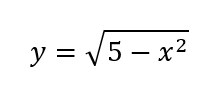Ableitung mit Wurzel berechnen

Question

Weiß jemand, wie man hier die Ableitung berechnet? 

Mein Lösungsansatz wäre eigentlich: Innere Ableitung (was in der Wurzel steht) mal äußere Ableitung (gesamter Ausdruck; allerdings zunächst umgeschrieben (statt Wurzel: hoch(1/2)). Aber ich weiß halt nicht, ob es so tatsächlich richtig wäre.

:)

 

Comments

Vielen Dank euch für die Antworten! :)

Answer 1

y'=-2x/(2√(5-x^2))=-x/√(5-x^2)

Answer 2

y= (5-x^2)^{1/2}

y'= 1/2 (5-x^2)^{-1/2} * (-2x)

y '= (-x)/(√(5-x^2))

Answer 3

$$ y = \sqrt{5-x^2} \\ y' = -2x \cdot \dfrac{1}{2 \cdot \sqrt{5-x^2} } = \dots $$Der Ansatz ist gut. Man muss die Wurzel nicht umschreiben, sie kommt ja oft genug vor, so dass man ihre Ableitung wissen darf.

Answer 4

Allgemein
( √ term ) ´ = ( term ´ ) / ( 2 * √ term )

term = 5 - x^2
term ´= - 2x
( √ ( 5 - x^2 ) ) ´ = ( -2x ) / ( 2 * √ ( 5 - x^2 ) )
( √ ( 5 - x^2 ) ) ´ = ( -x ) / √ ( 5 - x^2 )