Achterbahn: Wie steil ist es in den angegebenen Punkten? y=-1/6x^3+x

Question

Aufgabe:

Das Bild zeigt einen kleinen Ausschnitt einer Achterbahn. Ein Teilstück einer solchen Achterbahn kann durch die Funktion \( y=-\frac{1}{6} x^{3}+x \) im Intervall \( [0 ; 2,5] \) beschrieben werden (x und \( y \) jeweils in 10m-Einheiten).

a) Wie steil ist es in den angegebenen Punkten?

b) An welcher Stelle liegt der höchste Punkt? Benutze zum Finden dieses Punktes auch die Steigung.

c) An welchen Stellen vermutest du das größte Gefälle und die größte Steigung? Berechne je einen Näherungswert für diese Steigungen.

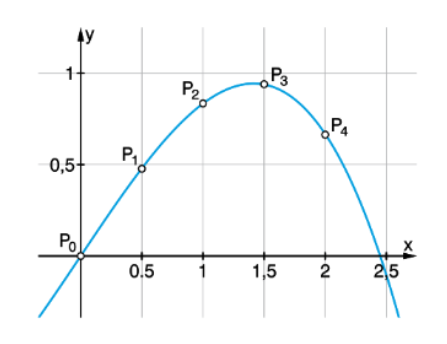
Ansatz:

Bei a) komme ich auf das Ergebnis 1 dies habe ich von der Funktion abgelesen.

Bei b) komme ich auf das Ergebnis 0,3.

Bei c) komme ich gar nicht weiter, ich weiss nicht wie ich anfangen soll.

Ich bitte um eine nachvollziehbare Lösung.

Comments

Das Bild zeigt einen kleinen Ausschnitt einer Achterbahn. Ein Teilstück einer solchen Achterbahn kann durch die Fkt. - 1/6 * x3 + x im intervall 0;2,5 beschreiben werden.

Answer 1

f ( x ) = - 1/6 * x^3 + x
f ´ ( x ) = -1/2 * x^2 + 1

Zur Beantwortung der Aufgabe ist die Differentialrechnung
vonnöten.

Bei a) komme ich auf das Ergebnis 1 dies habe ich von der Funktion abgelesen.

f ´( 0.5 ) = -1/2 * 0.5^2 + 1
f ´( 0.5 ) = -0.125 + 1 = 0.875

Bei b) komme ich auf das Ergebnis 0,3.

Hochpunkt
f ´( x ) = 0
-1/2 * x^2 + 1 = 0
x = √ 2 = 1.414
H ( 1.414 | f ( 1.414 ) )

Bei c) komme ich gar nicht weiter, ich weiss nicht wie ich anfangen soll.

Steilster Anstieg
f ´ ( 0 ) = ???
Steilstes Gefälle
f ´( 2.5 ) = ???