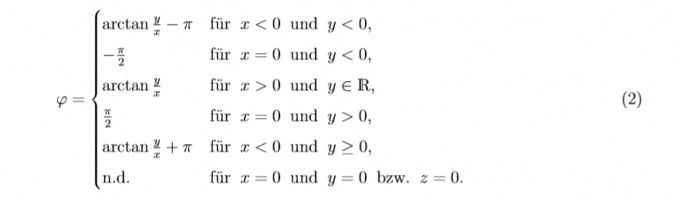ich soll den WInkel phi der komplexen Zahl -3-3i bestimmen.
arctan(-3/-3)= 0,785398163 geteilt durch π damit phi= 1/4π. Da Realteil und Imaginärteil kleiner als 0 sind müsste ich ja π abziehen um auf phi= -3/4π zu kommen
In der Lösung steht jedoch 5/4 π, also + 1π.
wieso wird hier denn nicht wie in der Formelsammlung arctan y/x-π benutzt wenn Realtiel und Imaginärteil kleiner als 0?