Ich habe folgende Aufgabe bekommen und habe auch einen Ansatz wie ich vorgehen kann, aber komme dann an einer Stelle nicht mehr weiter. Vielleicht könnte mir da jemand behilflich sein.
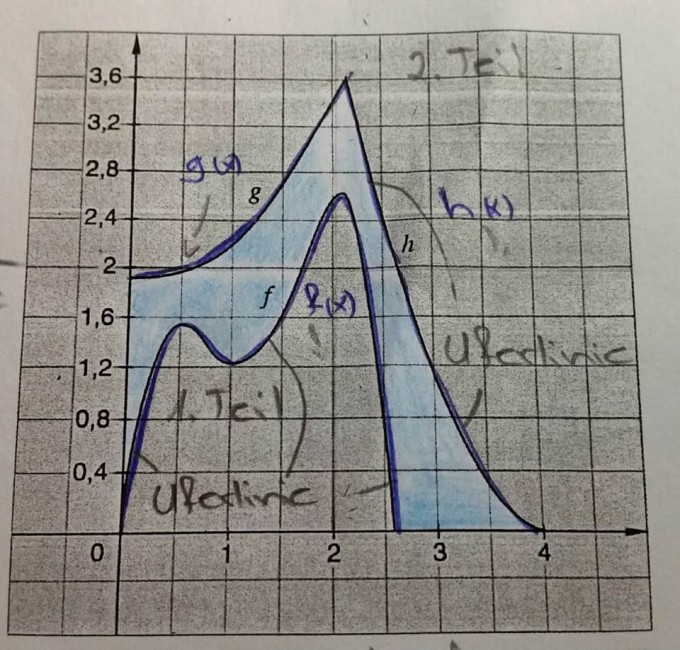
Ein Golfplatz ist durch einen See wie in der Grafik zweigeteilt (Grafik im Anhang). Der inselartig geformte Teil des Golfplatzes wird durch ein Ufer begrenzt, dessen Uferlinie der Funktion f(x) = -2x^4+28/3x^3-14x^2+8x entspricht.
Der Hauptteil des Golfplatzes liegt nördlich auf dem Festland, seine Uferlinie ist durch die Funktion g(x) = 0,5x^2-0,25x+2; 0<x<2 und h(x) = x^2-8x+16; 2<x<4 gekennzeichnet.
Eine Einheit entspricht 100 Metern. Berechnen Sie die Fläche des Sees, der von den Uferlinien und beiden Koordinatenachsen begrenzt sind.
Meine Grundidee war, dass ich den kompletten Flächeninhalt "der Grafik" und die Flächeninhalte von f(x), g(x) und h(x) berechne und dann den gesamten Flächeninhalt von den anderen abziehe. Das habe ich auch getan und hab als Ergebnisse f(x)=4,12m^2, g(x)=4,82m^2 und h(x)=74,83m^2. Spätestens an dieser Stelle ist mir klar geworden, dass das so nicht funktionieren kann, aber leider weiß ich gerade auch nicht wie ich es richtig machen kann. Vielleicht könnte mir da jemand einen Ansatz geben oder einen groben Plan wie ich hier vorgehen muss.