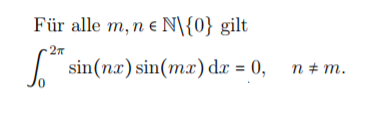Symmetrie in der Integralrechnung

Question

Hi, ich habe hier eine Aufgabe wo ich nicht genau weiterkomme.

Meine Idee war es zu zeigen, dass auf dem Intervall [0,pi] (also[0,pi/2],[pi/2,pi]) eine Punktsymmetrie vorliegt und somit für m !=n nur die 0 als Ergebnis rauskommen kann, denn die Integrale heben sich ja gegenseitig auf.

Nur wie zeige ich dies?

Aufgabe:

Answer 1

gemäß Additionstheorem ist

$$ sin(nx)sin(mx)=\frac{1}{2}[cos((m-n)x)-cos((m+n)x)] $$

Integriere nun!

Comments

Danke für die rasche Antwort, ginge es denn nicht mit der Symmetrie?

Ich fände diesen Weg vielleicht etwas eleganter, denn dieses Monster dort zu Integrieren, wird haarig.

---

Das Teil ist ganz easy zu integrieren, dass sind nur elementare Cosinusfunktionen ... ;)

Eine Stammfunktion lautet:

$$ \frac{1}{2}[sin((m-n)x)/(m-n)-sin((m+n)x)/(m+n)] $$

und da m und n natürliche Zahlen sind kommt im Sinus für x=0 und x=2π jeweils 0 raus und alles wird 0 

Mit der Symmetrie komme ich nicht hin, betrachte z.B f(x)=sin(3x)sin(x)

https://www.wolframalpha.com/input/?i=plot+sin(3x)sin(x),+0%3C%3Dx%3C%3Dpi