Zerfall über die Halbwertzeit
Halbwertzeit Polonium 138 Tage
N ( t ) = N0 * 1/2 ^{t/138}
Alle Exponentialfunktionen kann man in eine
andere Exponentialfunktion mit anderer Basis
umwandeln z.B. die Basis e.
N ( t ) = N0 * 1/2 ^{t/138}
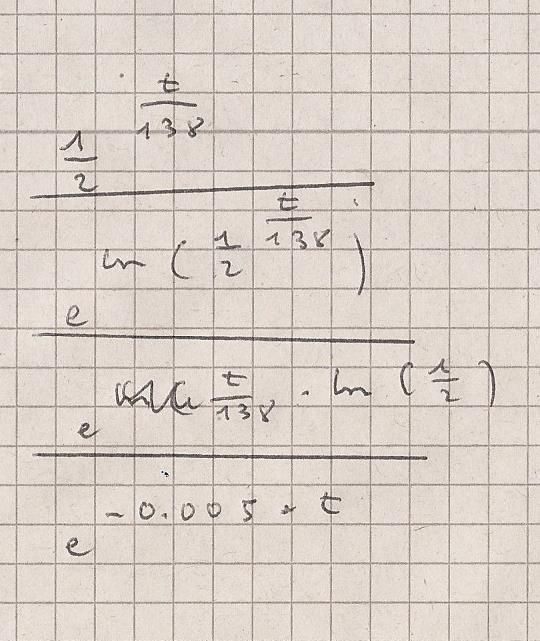
N ( t ) = N0 * e^{-0.005*t}
Okay, danke. Aber wann benutzt man dann die
Gleichung mit der e-Funktion?
Beide Schreibweisen sind gleichwertig.
Ist die Halbwertzeit gegeben kann man die erstgenannte
Funktion mit 1/2 nutzen.
Ist lambda gegeben kann man die e-Funktion direkt
nutzen.