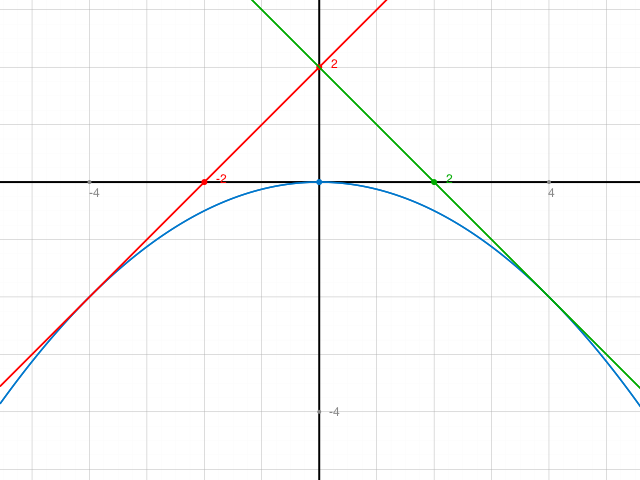
gegeben ist f(x)= -1/8 x²
Bestimme t und Berührpunkt der Geraden g: y= mx+2.
t soll vermutlich die Tangente sein. Eine von den g: y = mx+2.
Wichtig: Graph von f und t haben genau einen gemeinsamen Punkt.
Also: Funktionsgleichungen gleichsetzen und dafür sorgen, dass die quadratische Gleichung genau eine Lösung hat.
Erreicht man, indem man die Diskriminante 0 setzt.
-1/8 x^2 = mx + 2
0 = 1/8 x^2 + mx + 2 |*8
0 = x^2 + 8mx + 16
a=1, b=8m, c = 16
d = b^2 - 4ac = 64m^2 - 64 = 0
-------> m = ±1
t1 : y = x+2
t2: y = -x + 2
Jetzt noch die Berührpunkte berechnen.
-1/8 x^2 = x + 2
0 = 1/8 x^2 + x +2
0 = x^2 + 8x + 16 = (x+4)^2 → x = - 4, y = -4 +2 = -2. B1 (-4, -2)
-1/8 x^2 = -x + 2
0 = 1/8 x^2 -x +2
0 = x^2 - 8x + 16 = (x-4)^2 → x = 4, y = -4 +2 = -2. B2 (4, -2)
Kontrolle: Graph