Berechnung der Kantenlänge eines regelmäßigen Tetraeders

Question

Alle warten auf neue Fragen ... hier ist eine:

Vier gleich große Golfbälle mit dem Durchmesser d sollen verpackt werden. Um interessant und damit verkaufsfördernd zu wirken, soll die Verpackung ein regelmäßiges Tetraeder sein.

Einfache Frage: Welche Kantenlänge muss dieses Tetraeders mindestens haben?

Answer 1

Na da tischt du uns ja einen schönen Brocken auf :) Aber eine interessante Aufgabe. Ich probiere es mal:

Wenn wir uns ein Tetraeder vorstellen der alle Kugelmittelpunkte verbindet hat der die Kantenlänge d. Damit gilt für die Höhe

H1 = √6 / 3 * d

Denken wir uns jetzt um eine Kugel als Inkugel einen Tetraeder. Dann gilt für die Höhe des Umliegenden Tetraeders.

H2 = 2 * d

Nun müsste sich die gesamte Höhe aus H1 und H2 zusammensetzen lassen. 

H = H1 + H2 = √6 / 3 * d + 2 * d = (√6 / 3 + 2) * d

Daraus können wir jetzt wieder ein Rückschluss auf die Kantenlänge des äußeren Tetraeders ziehen.

a = √6 / 2 * H = √6 / 2 * (√6 / 3 + 2) * d = (√6 + 1) * d

Die Kantenlänge des Tetraeders sollte also etwa das 3.45 fache der Kugelradien betragen.

Kommt das in etwa hin ?

PS: Formeln habe ich soweit nötig von: http://www.mathematische-basteleien.de/tetraeder.htm

Comments

Die Kantenlänge des Tetraeders sollte also etwa das 3.45 fache der Kugeldurchmesser betragen. ;)

 

Dann passt ja unsere Rechnung, zumindest haben wir das Gleiche^^.

---

Ja, genau, das ist die Lösung! Toll, dass ihr das so schnell herausbekommen habt!

Allerdings hätte ich gern noch ein paar mehr Berechnungen dazu gesehen ...

Dies mache ich nun zum Kriterium für die Vergabe der "Besten Antwort " und da gewinnt eindeutig Der_Mathecoach.
Sorry, lieber Unknown, aber irgendwie muss ich meine Auswahl ja treffen ...

Answer 2

Hi,

sehr aufmerksam von Dir :D.

 

Ich würde die vier Golfbälle mal stapeln und man erkennt zwei Tetraeder. Den Tetraeder gebildet durch alle Mittelpunkte und den Tetraeder gebildet durch ein Außentetraeder (an welchem wir Interesse hegen).

Dank dem Innentetraeder haben wir r ins Spiel gebracht.

Leicht lässt sich dann die Höhe des gesamten Tetraeders berechnen:

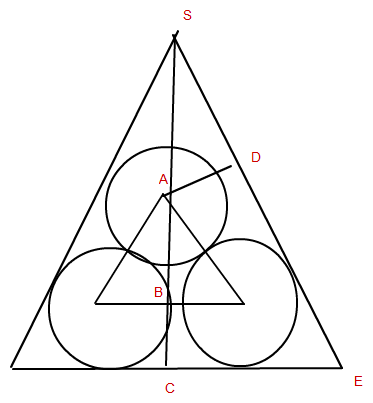
(Ich hoffe mir werden meine zeichnerischen Fähigkeiten nachgesehen :P.

BC ist schlicht r

AB ist die Höhe des Innentetraeders, also auch kein Problem

SA lässt sich dank Dreieck SAD berechnen, dabei sollte man allgemein über das Außendreieck an die Sache herangehen (SCE).

 

Hoffe das hilft schon weiter. Ich schau mal was ich für a=SE rausbekomme.

--> Komme auf a = (√6+1)2r = (√6+1)d

 

Grüße

Comments

 

ich habe exakt dieses Problem (als Präsentation für Mathe) ... Plus noch viel mehr Berechnungen, die aber (für mich) alle machbar sind.

Nur die Kantenlänge des Umtetraeders ist ein Problem (für mich), leider auch nach Durchsicht der hier vorgestellten Lösungen. Ich kann sie überhaupt nicht nachvollziehen. Zum Beispiel verstehe ich nicht, was der Punkt D in der Zeichnung ist.

Wäre es möglich, die Rechnungsschritte für "Normalsterbliche" etwas nachvollziehbarer zu gestalten?

Tausend Dank!!!

---

Wo hängt es denn? Gebe zu, dass es keine Schönheit ist, wie ich das aufgeschrieben habe und musste es auch nochmals kurz angucken.

BC und AD sollten kein Problem sein?

D liegt so, dass AD senkrecht auf SE liegt und wir so AD = r haben. Dann haben wir mit SAD ein rechtwinkliges Dreieck, wo AD = r ist, zudem muss der Winkel an S 30° betragen (gleichseitiges Dreieck). Dann können wir auch SA berechnen und haben die Höhe des Außentetraeders und damit die Kantenlänge

---

Ich habe es verstanden! Ich habe nicht erkannt, dass D derjenige Punkt ist, wo die Kugel den Außentetraeder berührt ... mit deiner Hilfe konnte ich alles nachvollziehen. VIELEN Dank!!!  Thorsten  :-)

---

Das lag an meiner Skizze. Nicht sonderlich sauber. Verzeih.

Gerne :)

---

Ich hab hier

https://www.mathelounge.de/443725/pyramide-aus-vier-kugeln-kantenlange-des-tetraeders-gesucht?show=444305#a444305

eine GeoGebra Zeichnung dazu gemacht - vielleicht hilfts?