Kreisberechnung - Aufgabenstellung

Question

In Sophias Garten soll ein kreisrunder Swimmingpool mit einem Durchmesser von 5 Metern errichtet werden. Das Material für eine Abdeckplane wird in Form einer 13,53 m langen und und 1,85m breiten Rolle geliefert.

1) Reicht das Material aus, damit der Swimmingpool vollständig abgedeckt werden kann? Begründet die Antwort durch eine Rechnung! 

2) Gebt mindestens eine Möglichkeit an, wie die Plane zusammengenäht werden muss, damit sie möglichst wenige Nahtstellen aufweist und doch den gesamten Pool abdeckt! 

Answer 1

$$A=π \cdot \left(\frac{d}{2}\right)^2  $$$$A=π \cdot \left(\frac{5m}{2}\right)^2 \approx 19.64m^2 $$

Nun muss noch die Quadratmeter für die Plane bestimmt werden:$$ {A}_{Plane}=13.53m \cdot 1.85m \approx 25.03m^2 $$

Das heißt das es aussreicht.

Die b) würde ich wie folgt angehen:$$d=\sqrt[]{\frac{25.03}{π}\cdot 4} \approx 5.65m$$

Es wäre also am besten eine Plane mit dem Durchmesser von 5.65m zu nehmen

Liebe Grüße

Comments

Danke:) Aber wie bist du auf die 4 bei der Berechnung des Durchmessers draufgekommen?

---

Das ist die Formel für die Flächenberechnung beim Kreis$$  A=π \cdot \left(\frac{d}{2}\right)^2 $$ Die habe ich nun umgestellt:$$  A=π \cdot \left(\frac{d}{2}\right)^2 \quad |:π $$$$\frac{A}{π}=\left(\frac{d}{2}\right)^2  \quad |\left(\frac{d}{2}\right)^2→ \frac{d^2}{4}  $$$$\frac{A}{π}=\frac{d^2}{4}  \quad | \cdot 4  $$$$d^2=\frac{A}{π} \cdot 4  \quad |\sqrt[]{}  $$$$d=\sqrt[]{\frac{A}{π} \cdot 4} $$ Dadurch habe ich dann den Durchmesser bestimmt:$$d=\sqrt[]{\frac{25.03}{π} \cdot 4} \approx 5.65m $$ 

Answer 2

A=πr^2

A=π*(2,5m)^2

A=25/4 πm^2≈19,63m^2

A=a*b

A=13,53m*1,85m

A=25,03m^2

Ja, die Plane reicht aus.

Smitty

Answer 3

Ich denke es ist folgendermaßen

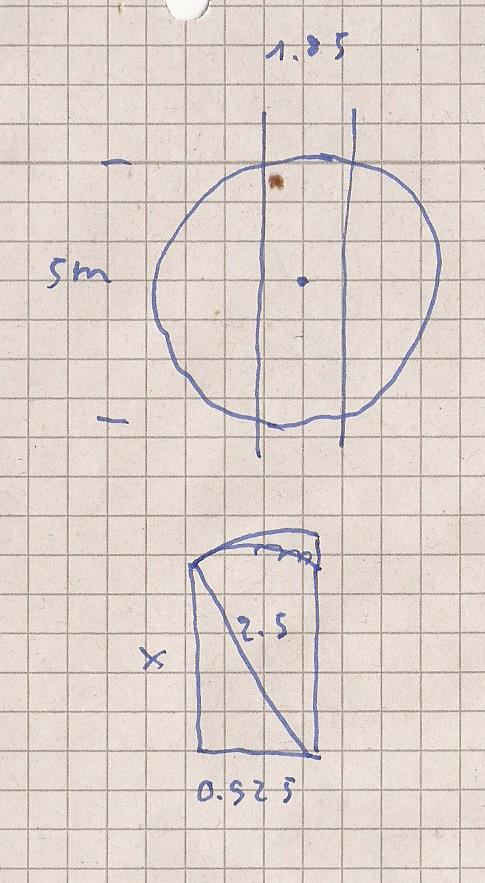
Die erste Skizze zeigt die erste mittig verlegte Bahn
von 5 m Länge.

Die Länge x auf der 2.Sizze zeigt wo diese Bahn mit
dem Linken Rand den Poolrand schneidet.

2.5 ^2 = ( 1,85 / 2 ) ^2 + x^2
x = 2.32 m
Die nächste linke Bahn hätte 2.32 ( obere Hälfte ) + 2.32 ( untere
Hälfte ) Länge = 4.64 m

Zur vollständigen Abdeckung des Pools sind
3 Bahnen erforderlich
4.64 m + 5 m + 4.64= 14.28 m

Dies ist mehr als die gegebene Länge von
13.53 m.

Es sind vielleicht noch andere Stückelungen möglich
aber jetzt ist es zu spät am Abend.

Comments

Hier eine Möglichkeit

Die ersten beiden Bahnen ( 5 m ) werden links
und rechts der Mitte verlegt.

Am linken und rechten Rand beträgt die
abzudeckende Länge
l = √ ( 2.5 ^2 - 1.85 ^2 )
l = 1.68 m
Nach oben und unten
l = 3.36 m

Übrig geblieben sind 13.53 - 10.00 = 3.53 m
Notwendige Breite
2.5 - 1.85 = 0.65 m
Das übrig gebliebene Stück Folie wird der Länge
nach halbiert und hat dann die Maße
3.53 * 0.925 m
benötigt
3.36 mal 0.65 m
Die 2 entstandenen Folien passen also.