Hallo alirizzo ,
f(x) = 3*x-2 = 3/x2 g(x) = 2 - 1/4 * x2
2 - 1/4 * x2 = 3 / x2 | * x2
2x2 - 1/4 x4 = 3 | -3 | umstellen
-1/4 x4 + 2x2 - 3 = 0 | * (-4)
x4 - 8x2 + 12 = 0
Setze z = x2
z2 - 8z + 12 = 0
$$ z^2 + p \cdot x + q = 0 $$pq-Formel: p = - 8 ; q = 12
$$ z_{1,2} = -\frac { p }{ 2 } \pm \sqrt{ \left(\frac { p }{ 2 }\right)^2-q} $$
z1,2 = 4 ± 2
z1 = 6 , z2 = 2
Resubstitution:
x2 = 6 oder x2 = 2
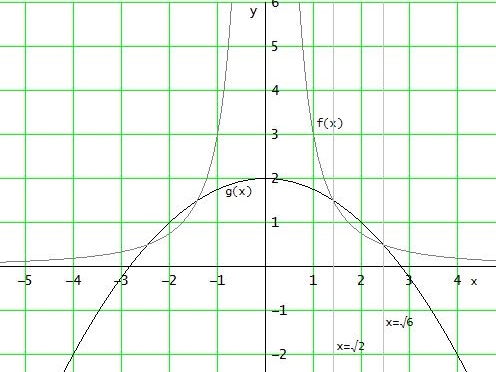
x1,2 = ± √6 , x3,4 = ± √2
Gruß Wolfgang