Schnittpunkt Pr : f(x) = gr(x)
(4 - ex)·ex = r·ex | : ex
4 - ex = r
ex = 4 - r | ln(...)
x = ln(4 - r)
Graphen für r = 2:
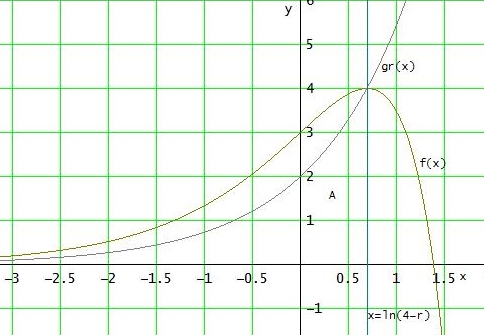
Gesuchte Fläche Ar :
$$ A_r=\int_{0}^{4-ln(r)} \! r·e^x \, dx=[r·e^x]_0^{ln(4-r)}= r·(4-r)-r=3r-r^2$$$$ A_r ' = 3-2r = 0 \text{ }\text{ }→ \text{ }\text{ } r=1,5\text{ } \text{ }(für\text{ } maximale \text{ }Fläche)$$Gruß Wolfgang