Hallo Meroo,
Die Rasenpyramide sieht im Prinzip so aus (klick auf das Bild und rotiere die Szene mit der Maus)
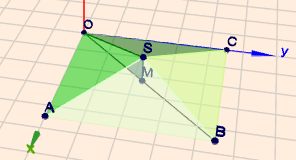
Die Punkte der quadratischen Grundfläche habe ich mit \(OABC\) bezeichnet. Die Spitze sei \(S\). Ich unterstelle, dass sich \(S\) direkt oberhalb der Mitte \(M\) der Grundfläche befindet. Die Länge der Diagonal \(OB\) erhält man über den Pythagoras
$$|OB| = \sqrt{|OA|^2 + |AB|^2} = \sqrt{45^2 + 45^2} \text{m} \approx 63,64\text{m}$$
Die Strecke \(OM\) ist halb so lang wie \(OB\). Das Dreieck \(\triangle OMS\) habe ich Dir nochmal raus gezeichnet
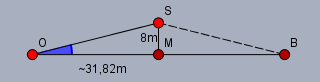
Der Tangens des blau markierten Winkels \(\alpha\) ist Gegenkathete \(MS\) zu Ankathete \(OM\). Also ist
$$\alpha = \arctan \frac{|MS|}{|OM|} = \arctan \frac{|MS|}{\frac12\cdot |OB|} \approx \arctan \frac{8}{31,82} \approx 14,1°$$
zu b) das Volumen einer Pyramide \(V\) berechnen sich aus einem Drittel von Höhe mal Grundfläche - also hier
$$V = \frac13 \cdot 8\text{m} \cdot (45\text{m})^2 = 5400\text{m}^3$$