Dreiseitige Pyramide: Punkt P auf Kante AB mit geringsten Abstand von S gesucht

Question

ich komme bei folgender Aufgabe nicht weiter,

geg. dreiseitige Pyramide mit Eckpunkte A (2|1|-1), B (8|7|0), C (0|9|1) und S (4|4|10)

gesucht: Punkt P auf der Kante AB, der vom Punkt S den geringsten Abstand hat

!

Answer 1

Vielleicht hilft es sich einen Plan zu machen?

Die Grundaufgabe lautet Abstand Punkt P - Gerade AB

Comments

Danke, ich hab es mir natürlich auch vorher aufgezeichnet. Wenn ich aber Abstand Punkt-Gerade anwende, erhalte ich einen Punkt außerhalb der AB Kante...

---

Das kann nicht sein, weil Deine Gerade AB ist. Auf der ist der Lotfußpunkt von S zu bestimmen:

g(t) = A + t (B-A)  {F=g(to) ein Punkt auf der Geraden}

Von F senkrecht hoch zu S, d.h. der Vektor \(\vec{FS} \) ist senkrecht zum Richtungsvektor der Geraden \(\vec{AB} \). Jetzt ist für F=g(to) das to so ein zurichten, dass die Vektoren senkrecht stehen - das Skalarprodukt = 0 ist.

Schaffst Du das?

---

Als Fußpunkt kommt ja F(2+6r|1+6r|-1+r)

Das ins Profukt mit dem Normalvektor der Gerade AB (6; 6; 1) mit 0 setzen, kommt r=-17/73 und der Punkt (0,6|-0,4|-1,23).

Zwar liegt der Punkt auf der GERADEN AB aber  ja außerhalb des Intervalls von AB (Kante AB)

Hab ich mich eventuell irgendwo verrechnet?

---

HM,

scheint so, ich komm auf r = 41 / 73

Du musst den Vektor SF = Sg(r) = S-g(r) nehmen nicht g(r) selber! Dann wird das was...

---

Dann kommt ja nur noch entweder A oder B als nächsten Punkt zu S in Frage, wenn der Punkt außerhalb der Kante liegt, oder?

P.S.: Es handelt sich auch um eine "schwere" Leistungskursaufgabe...

---

Ganz bestimmt NICHT.

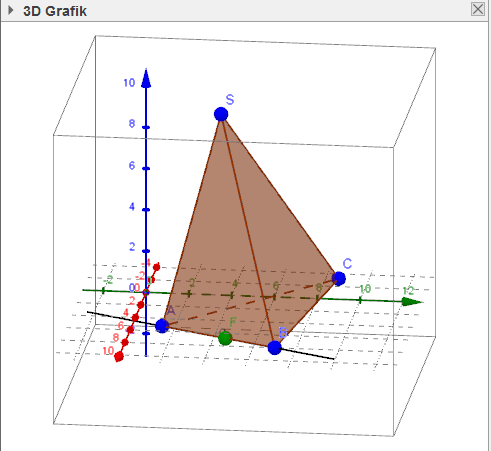
Der kürzeste Abstand der Kante AB zu S ist die Senkrechte von S auf die Gerade AB.

\( g(r) \, :=  \, \left( \begin{array}{r}6 \; r + 2\\6 \; r + 1\\ r - 1\\ \end{array} \right)   = F \)
F ein Punkt auf der 'Kante' AB, damit kontruierst Du einen Vektor SF der Skalar multipliziert mit dem Richtungsvektor der Geraden (6,6,1) = 0 ergeben muss - weil Senkrecht

\(  \left( \left( \begin{array}{r}6 \; r + 2\\6 \; r + 1\\ r - 1\\ \end{array} \right) - \left( \begin{array}{r}4\\4\\ 10\\  \end{array} \right)   \right)  \left( \begin{array}{r}6\\6\\ 1\\ \end{array} \right)  = 0   \)

Daraus erhältst Du (s.o.) r = 41 / 73 das ergibt

F=g(41/73) = \(   \, \left( \begin{array}{r}5.37\\4.37\\ -0.44\\ \end{array} \right)     \)