Sinusfunktion: Nullstellen und Extrema - k*2pi oder k*pi

Question

Aufgabe
f(x) = 2sin(2x-1) + 1

Bestimmen sie die Nullstellen und die Extrempunkte im Intervall [0,2π]

Nullstellen
0 = 2sin((2x-1) + 1
-1 = sin(2x-1) 
-90° = 2x-1
-90° + 1 = 2x
 ⇒ x_(N1) = -45° + 1/2*k2π = -45° + k*π

Graphisch finde ich x_(N2) bei

x_(N2) = 270° + 1/2 * k * 2π
x_(N2) = 270° + k*π

Frage: Kann das bis hier sitmmen?

Extremalstellen

f'(x) = 4cos(2x-1)
0 = f'(x)
0 = cos(2x-1)
90° = 2x-1 
90 + 1 = 2x
x_(E1) = 45° + 1/2 * k * 2π = 45° + kπ

270° = 2x-1 (Graphisch gefunden)
x_(E2) = 135° + 1/2 * k * 2π = 135° + k*π

Frage: Wie finde ich jetzt mit Gradwerten heraus was ein Hoch bzw. Tiefpunkt ist? Oder muss ich sagen ich nehme die f"(x_(E)) ≠ 0 und über prüfe so indem ich die pi-werte brauche?

Comments

Wie finde ich jetzt mit Gradwerten heraus was ein Hoch bzw. Tiefpunkt ist?

Zwischen Bogenmass und Grad kann man mit einem Dreisatz umrechnen. 

Du solltest keine "Mischungen" verwenden. 

---

0 = 2sin((2x-1) + 1
-1 = sin(2x-1) 

muß es nicht heißen
0 = 2sin((2x-1) + 1
-1/2 = sin(2x-1) 

---

jawohl, -1/2 wäre richtig gewesen

Answer 1

> -90° = 2x-1 

Verwende Bogenmaß:

    -π/2 = 2x-1

Periodizität würde ich auch direkt mit einbringen:

    -π/2 + 2πn = 2x-1 , n∈ℤ

Nach x auflösen liefert

    -π/4 + πn + 1/2 = x, n∈ℤ

Einsetzen zeigt, dass x für n ∈ {1, 2} im Definitionsbereich liegt.

Allerdings hast du schon

        0 = 2sin(2x-1) + 1 

falsch umgeformt. Korrekt umgeformt ergibt das nämlich

        -1/2 = sin(2x-1).

-1/2 taucht pro Periode zwei mal als Funktionswert der Sinusfunktion auf, also

    -π/6 + 2πn = 2x-1 oder -5π/6 + 2πn = 2x-1, n∈ℤ

Comments

Okay, wenn ich es sofort in RAD aufschreiben will kommt bei mir natürlich nicht so ein schöner wert raus wie -π/2.

(1.) Im Rad-Modus im TR Wie folgt eingegeben:
-(1/2) = sin(u)   I sin^{-1}
-0.523598776 = u 

(2.) Im Deg-Modus im TR wie folgt eingegeben
-(1/2) = sin(u)  I sin^{-1}
-30 = u 

π = 180° 
π/2 = 90°
π/2 * 1/3 = 30°
π/6 = 30°
⇒ -π/6 = -30°

Dann rechne ich mit dem Wert -π/6 also weiter?


Und gibt es irgendwo Lösungen zu dieser aufgabe?

---

Der CASIO fx-CG 20 liefert bei Eingabe von

sin

^-1(-1/2)

die Ausgabe

-1/6 π

> Dann rechne ich mit dem Wert -π/6 also weiter? 

Auf jeden Fall.

Für ganzzahlige Vielfache von 30° und 45° sollte man allerdings nicht auf einen Taschenrechner angewiesen zu sein, um trigonometrische Funktionen zu berechnen.

---

Ok meiner ist ein Texas Instruments Ti-30 ECO RS :-/ der zeigts leider nicht so an, wie deiner. 

Auf jeden Fall mache ich die Umkehrfunktion im Deg und rechne dann ins Bogenmass um. 

Vielen Dank Oswald

Answer 2

0 = 2 * sin (2x-1) + 1
Ich gehe einmal davon das die Angaben in
Bogenmass sind. Die letzte 1 wäre bei
Angaben in Grad ein relativ kleiner und
unbedeutender Wert.
Ebenso wurde das Intervall in Bogenmass
angegeben.

sin(2x-1) = -1/2  | arcsin
2x - 1 = -0.524
x = 0.24

Dies ist eine Stelle, da gibt es noch ein paar mehr.

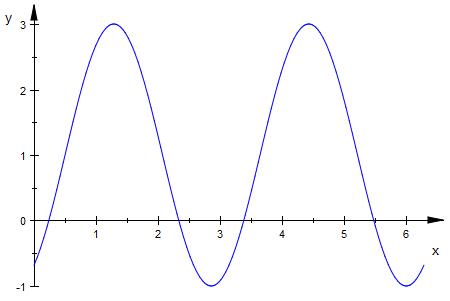
Extremwerte ( alle )
f(x) = 2sin(2x-1) + 1
f ´( x ) = 2 * cos(2x-1) * 2
f ´( x ) = 4 * cos(2x-1)

4 * cos(2x-1)  = 0
cos(2x-1) = 0  | arccos
Die cos Funktion ist 0 bei
1 / 2 * π , 3 / 2 * π , 5 / 2  * π , 7 / 2  * π , 9 / 2  * π
2x - 1 = 1/2 * π
x = 1.29
2x - 1 = 3/2 * π
x = 2.86
2x - 1 = 5/2 * π
x = 4.43
2x - 1 = 7/2 * π
x = 6

Comments

was genau passiert ab diesem Schritt, hier kriege ich:

Cos(u) = 0

u = π/2 + k*2*π | u = 2x-1

2x - 1 = π/2 + k*2*π

2x = π/2 +1 + k*2*π | :2

x = π/4 +1/2 + k*π wobei k∈ℤ

⇒ x_(1) = π/4 +1/2

⇒ x_(2) = π/4 +1/2+π

oder?

---

arcsin (-1/2 ) = -0.524

Die sin-Kurve ist achsensymmetrisch zu x = π / 2
Von -0.524  zu π / 2 sind es : d = 2.095
Die nächste Schnittstelle wäre
π / 2 + d = π / 2 + 2.095 = 3.67
Alle Schnittstellen
-0.524
3.67
-0.524 + 2 * π
3.67 + 2 * π
usw
x ausrechnen
2x - 1 = -0.524
x = 0.24
und prüfen ob im Intervall [ 0 ; 2π ]