Ich schreibe mal x für a, weil das bei Funktionen so üblich ist.
und zeichne
y = (3/-2) x2 = -1.5 x2 Parabelgleichung.
Scheitelpunktform y = -1.5 (x-0)2 + 0
und
y = 1 Geradengleichung
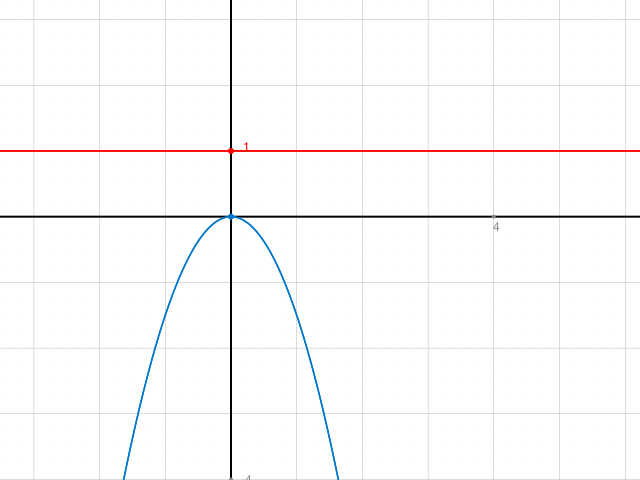
Hier sieht man, dass die Parabel nach unten geöffnet ist und S(0/0) der Scheitelpunkt ist.
Es ist niemals möglich, dass die Parabel die horizontale Gerade schneidet.
Deshalb hat die angegebene Gleichung keine Lösung.
Du wolltest ja eigentlich rechnen!
(3/-2) a2 = 1. Gesucht a
-1.5 a2 = 1 |: (-1.5)
a2 = - 0.666666666
Unlösbar, wenn a reell sein soll, da beim Quadrieren keine negativen Werte rauskommen.