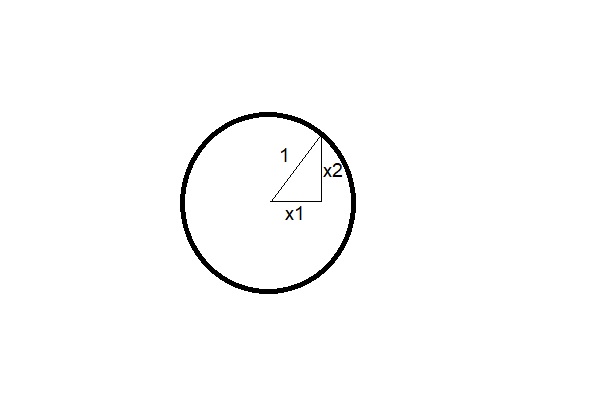einheitskugel und Funktion mit Variablen skizzieren

Question

a.) Skizziere für $$ p=1,\quad 2,\quad 3,\quad \infty $$ jeweils die Einheitskugel $$ B\_ p=\left\{ x\quad \in \quad R²\quad :\quad ||x||\_ p\quad \le \quad 1 \right\} $$ in der Ebene.

Der Radius der Kugel ist 1, aber ich weiß nicht was p sein soll ?

b.) Skizziere die Definitionsmenge der Funktion:

$$ f(x,y)=\frac { \sqrt { ln((x-1)² +y²-4) }  }{ y-x } $$

Ich hab die Funktion auf Wolframalpha geplottet, aber das sieht nach etwas aus, was ich nicht mit der Hand zeichnen kann.

Oder was ist mit der Definitionsmenge gemeint ?

Comments

Der Radius der Kugel ist 1, aber ich weiß nicht was p sein soll ?

p ist der Reihe nach 1, 2, 3, ∞. Das gibt also vier Zeichnungen. Die Definition der p-Norm schlaegst Du nach, wenn Du es nicht weisst.

Oder was ist mit der Definitionsmenge gemeint ?

Die Menge der Punkte (x, y), für die die Funktion definiert ist. Das ist eine ebene Menge. Du sollst nicht den Graphen der Funktion zeichnen.

---

Ich komme bei b.) nich weiter.

Hab jetz geschrieben D={x,y}inR² | y != x | (x-1)²+y²-4>0}

Weiß nich ob man das so schreiben darf.

Wie soll ich das im Kartesischen Koordinatensystem zeichnen ?`

Ich kann auch nicht nach y umformen, oder ich übersehe irgendwas.

---

Tipp: Kreisgleichung

Beachte desweiteren den Nenner in der ursprünglichen FUnktion, da fallen noch ein paar Punkte zum Schluss weg

---

$$ f(x,y) = \sqrt { \frac { ln((x-1)²+y²-4) }{ y-x }  } $$

 

Wenn ich das nach der Kreisgleichung umforme, komm ich auf:

$$ { e }^{ y-x }+4\quad =\quad (x-1)²+(y-0)² $$

Ich darf aber nich auf beiden Seiten der Gleichung x,y haben oder?

---

Da hast du meinen Tipp falsch verstanden ;)

(x-1)²+y²-4>0

ist als Bedingung aufgrund des ln erstmal richtig.

(x-1)²+y²-4=0 bwz  (x-1)²+y²=2^2 ist ein Kreis.

(x-1)²+y²> 2^2 ist dann alles außerhalb dieses Kreises.

Aufgrund des Nenners ist zusätzlich noch x≠y .Die Gerade y=x fällt also weg.

Answer 1

zu 1)

die Skizzen findest du oben in folgenden Link;

https://de.wikipedia.org/wiki/P-Norm

Comments

Schaut das immer so aus ?

Wie kann man das nachvollziehen, das die maximumsnorm, ein gleichseitiges Viereck ist ?

---

max(|x_1|,|x_2|) =1

bedeutet ja entweder ist |x_1| =1 und 0<=|x_2|<1 oder

|x_2| =1 und 0<=|x_1|<1.

Zeichne nun diese Fälle ein.

Answer 2

Hallo

das p als Index bezeichnet die Art der Norm

p=oo  ||x||=max( |x_1|,|x_2|)

p=1 ||x||=|x_1|+|x_2|

p=2 ||x||=\sqrt(x_1^2+x_2^2)

 was mit p=3 bezeichnet wird musst du in deinem skript nachsehen.

 2. Aufgabe: du sollst ja nicht die Funktion skiziieren sondern  die Menge (x,y) für die die Funktion definiert ist. d.h. untere der Wurzel darf nichs negatives stehen, im ln nicht 0 im Nenner nicht 0

Lies Aufgaben genauer!

Comments

Hey danke, ja leider gibt es bei uns kein Skript :(.

nun häng ich aber wie ich das zeichnen soll. Hab nur Beispiele mit Zahlen gesehn.

Es gillt also:

p=1 $$ ||x||_1=|x_1|+|x_2|\le 1$$

p=2 $$ ||x||_2=\sqrt{(x_1²+x_2²) }\le 1$$

p=3 $$ ||x||_2=³\sqrt{(x_1³+x_2³) }\le 1$$

p=oo $$ ||x||=max( |x_1|,|x_2|) \le 1$$

p=1 hab ich mal gezeichnet, aber bei den anderen bin ich irgendwie ratlos.

Ich weiß, dass p=2 der Pythagoras ist, aber wie soll ich das zeichen, auch versteh ich nich so ganz den sinn der Aufgabe. Was soll mir das zeigen.

---

Hallo

 p=1 ein Quadrat mit den Ecken auf den Achsen, bei + 1 und -1

p=2 Kreis richtig.

p=3 lass dir |x^3|+|y^3| plotten das gibt was wie ein abgerundetes Quadrat oder plattgedrückter Kreis,

p=oo

ein Quadrat mit den Switen x=1,x=-1, y=1,y=-1(also Seitenlänge 2)

Gruß lul