Es gibt bei a) und b) 100+19+10+1 = 130 Gewinne und 370 Nieten
(Habe erst nach Fertigstellung gemerkt, dass das Baumdiagramm bei dieser Fragestellung (ein relevanter Pfad!) etwas aufwändig ist :-))
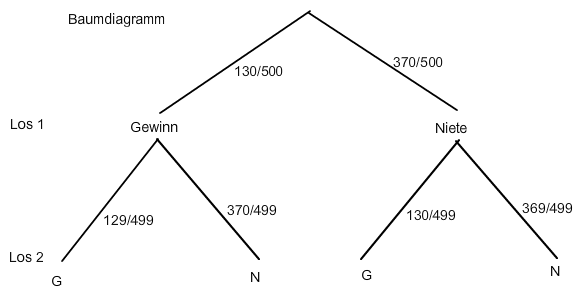
b)
Bei dem Pfad, der über zwei Nieten führt, sind die Wahrscheinlichkeiten an den Kanten zu multiplizieren:
P(" kein Gewinn") = 370/500 * 369/499 ≈ 0.547 = 54,7 %
a)
Gegenereignis zu b): P("mindestens 1 Gewinn") = 1 - P(" kein Gewinn") ≈ 0,453 = 45,3 %
c)
analog zu a): statt 130 hat man 30 Gewinne (+ 470 Nieten)
Gruß Wolfgang